Порядок выполнения действий

Порядок раскрытия скобок

Теперь рассмотрим порядок применения правил, разобранных выше в выражениях общего вида. То есть в выражениях, которые содержат суммы с разностями, произведения с частными, скобки в натуральной степени.

Порядок раскрытия скобок согласован с порядком выполнения действий:

• возвести многочлены в скобках в натуральную степень;
• слева направо провести умножение и деление;
• когда в скобках останутся только слагаемые, раскрыть скобки и привести подобные.

Пример 1. Раскрыть скобки и упростить выражение:

-(2a + 5b) + (3a — 2b + 1) — (2a + 4) = -2a — 5b + 3a — 2b + 1 — 2a — 4 = (-2a + 3a — 2a) + (-5b — 2b) + (1 — 4) = -a — 7b — 3

Пример 2. Доказать, что при любых значениях переменной a значение выражения 3(2a — 7) — (a — (5a + 4)) — отрицательно.

Доказательство:

3(2a — 7) — (a — 5(a + 1)) = 6a — 21 — a + 5(a + 1) = 6a — 21- a + 5a + 5 = (6a — a + 5a) + (-21 + 5) = 0 — 16 = -16

Значение выражения не зависит от переменной и всегда отрицательно. Что и требовалось доказать.

Второе правило раскрытия скобок

Здесь рассмотрим второе правило раскрытия скобок. Звучит так:

Второе правило раскрытия скобок Если перед скобками стоит знак минус — все числа, которые стоят внутри скобок, меняют свой знак на противоположный. Формула раскрытия скобок −(a − b) = −a + b

Например, раскроем скобки в выражении 5 − (−2 − 3)

Видим, что перед скобками стоит минус. Значит нужно применить второе правило раскрытия, а именно опустить скобки вместе с минусом, который стоит перед этими скобками. При этом слагаемые, которые были в скобках, поменяют свой знак на противоположный:

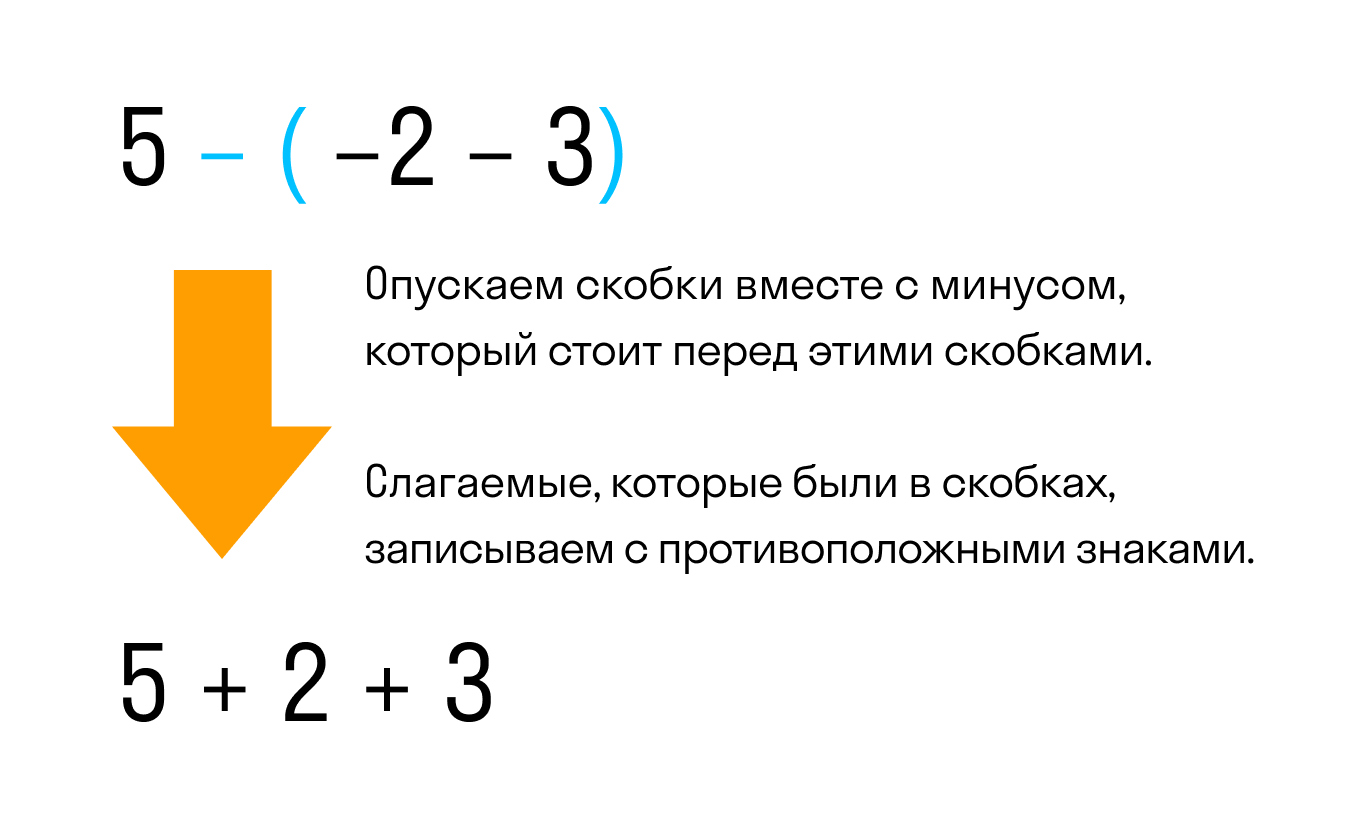
Так мы получили выражение без скобок 5 + 2 + 3. Это выражение равно десяти, как и предыдущее выражение со скобками было равно 10.

• 5 − (−2 − 3) = 10
• 5 + 2 + 3 = 10

Поэтому между выражениями 5 − (−2 − 3) и 5 + 2 + 3 можно поставить знак равенства так как они равны одному и тому же значению:

• 5 − (−2 − 3) = 5 + 2 + 3
• 10 = 10

Пример 1. Раскрыть скобки в выражении 18 − (−1 − 5)

Как рассуждаем:

Перед скобками стоит минус, поэтому применим второе правило раскрытия скобок:

18 − (−1 − 5) = 6 + 1 + 5

Пример 2. Раскрыть скобки −(−6 + 7)

Как рассуждаем:

Перед скобками стоит минус, поэтому применим второе правило раскрытия скобок:

−(−6 + 7) = 6 − 7

Пример 3. Раскрыть скобки −(−7 − 4) + 15 + (−6 − 2)

Как рассуждаем:

Здесь мы видим два места, где нужно раскрыть скобки. В первом случае применим второе правило раскрытия скобок, а во втором — первое правило:

−(−7 − 4) + 15 + (−6 − 2) = 7 + 4 + 15 − 6 − 2

Пример 4. Раскрыть скобки в выражении a − (3b + 3) + 10

Как рассуждаем:

Перед скобками стоит минус, поэтому применим второе правило раскрытия скобок:

a − (3b + 3) + 10 = a − 3b − 3 + 10

Порядок вычисления в выражениях со степенями, корнями, логарифмами и иными функциями

Если у нас в условии стоит выражение со степенью, корнем, логарифмом  или тригонометрической функцией (синусом, косинусом, тангенсом и котангенсом) или иными функциями, то первым делом мы вычисляем значение функции. После этого мы действуем по правилам, указанным в предыдущих пунктах

Иначе говоря, функции по степени важности приравниваются к выражению, заключенному в скобки

Разберем пример такого вычисления.

Пример 6

Условие: найдите, сколько будет (3+1)·2+623−7.

Решение

У нас есть выражение со степенью, значение которого надо найти в первую очередь. Считаем: 62=36. Теперь подставим результат в выражение, после чего оно примет вид (3+1)·2+363−7.

Дальше действуем по знакомому алгоритму: считаем, сколько у нас получится в скобках, потом в оставшемся выражении выполняем умножение и деление, а следом – сложение и вычитание.

(3+1)·2+363−7=4·2+363−7=8+12−7=13

Ответ: (3+1)·2+623−7=13.

В отдельной статье, посвященной вычислению значений выражений, мы приводим и другие, более сложные примеры подсчетов в случае выражений с корнями, степенью и др. Рекомендуем вам с ней ознакомиться.

Всё ещё сложно?
Наши эксперты помогут разобраться

Все услуги

Решение задач

от 1 дня / от 150 р.

Курсовая работа

от 5 дней / от 1800 р.

Реферат

от 1 дня / от 700 р.

Понятие раскрытия скобок

В задачах по математике постоянно встречаются числовые и буквенные выражения, а также выражения с переменными, которые составлены с использованием скобок.

Основная функция скобок — менять порядок действий при вычислениях значений числовых выражений. 

Часто можно перейти от одного выражения со скобками к тождественно равному выражению без скобок. Например:

2(3 + 4) = 2 * 3 + 2 * 4.

Такой переход от выражения со скобками к тождественно равному выражению без скобок несет в себе основную идею о раскрытии скобок.

Начальное выражение со скобками и результат, полученный после раскрытия скобок, удобно записывать в виде равенства, как мы это сделали в предыдущем примере.

В школе тему раскрытия скобок обычно подходят в 6 классе. На этом этапе раскрытие скобок воспринимают, как избавление от скобок, которые указывают порядок выполнения действий. И изучают раскрытие скобок на примерах выражений, которые содержат:

• знаки плюс или минус перед скобками, которые заключают сумму или разность, например, (a + 7) и -(-3 + 2a — 12 — b);
• произведение числа, одной или нескольких букв и суммы или разности в скобках, например, 3(2 — 7), (3 — a + 8c)(-b) или -2a(b + 2c — 3m).

Раскрытие скобок также можно рассматривать шире.

Раскрытием скобок можно назвать переход от выражения, которое содержит отрицательные числа в скобках, к выражению без скобок. Например:

5 + (-3) — (-7) = 5 — 3 + 7.

Или, если в описанных выше выражениях вместо чисел и переменных могут быть любые выражения. В полученных таким способом выражениях тоже можно проводить раскрытие скобок. Например:

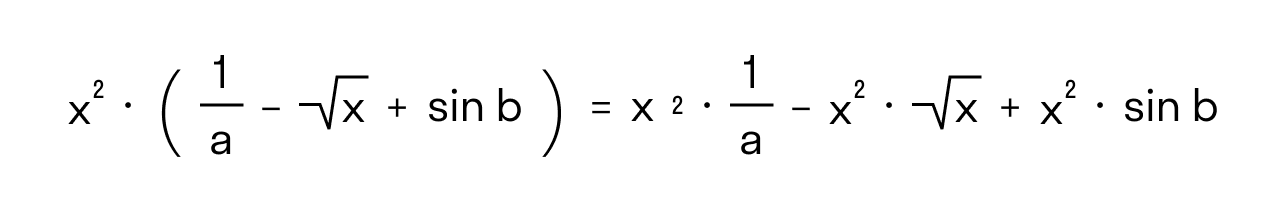
Раскрытие скобок — это избавление от скобок, которые указывают порядок выполнения действий, а также избавление от скобок, в которые заключены отдельные числа и выражения.

Важно отметить еще один момент, который касается особенностей записи решения при раскрытии скобок. При раскрытии скобок в громоздких выражениях можно прописывать промежуточные результаты в виде цепочки равенств

Например, вот так:

5 — (3 — (2 — 1)) = 5 — (3 — 2 + 1) = 5 — 3 + 2 — 1

Скобка в скобке

Иногда в практике встречаются задачи со скобками, вложенными внутрь других скобок. Вот пример такого задания: упростить выражение \(7x+2(5-(3x+y))\).

Чтобы успешно решать подобные задания, нужно:
— внимательно разобраться во вложенности скобок – какая в какой находиться;
— раскрывать скобки последовательно, начиная, например, с самой внутренней.

При этом важно при раскрытии одной из скобок не трогать все остальное выражение, просто переписывая его как есть. 
Давайте для примера разберем написанное выше задание.

Пример. Раскройте скобки и приведите подобные слагаемые \(7x+2(5-(3x+y))\).Решение:

\(7x+2(5\)\(-(3x+y)\)\()=\)		Выполнять задание начнем с раскрытия внутренней скобки (той, что внутри). Раскрывая ее, имеем дело только с тем, что к ней непосредственно относиться – это сама скобка и минус перед ней (выделено зеленым). Всё остальное (не выделенное) переписываем также как было.
\(=7x+2(5\)\(-3x-y\)\()=\)		Теперь раскрываем вторую скобку, внешнюю.
\(=7x+2·5-2·3x-2·y=\)		Упрощаем получившееся выражение…
\(=7x+10-6x-2y=\)		…и приводим подобные.
\(=x+10-2y\)		Готово.

Пример. Раскройте скобки и приведите подобные слагаемые \(-(x+3(2x-1+(x-5)))\).Решение:

\(-(x+3(2x-1\)\(+(x-5)\)\())\)		Здесь тройная вложенность скобок. Начинаем с самой внутренней (выделено зеленым). Перед скобкой плюс, так что она просто снимается.
\(-(x+3(2x-1\)\(+x-5\)\())\)		Теперь нужно раскрыть вторую скобку, промежуточную. Но мы перед этим упростим выражение привидением подобный слагаемых в этой второй скобке.
\(=-(x\)\(+3(3x-6)\)\()=\)		Вот сейчас раскрываем вторую скобку (выделено голубым). Перед скобкой множитель – так что каждый член в скобке умножается на него.
\(=-(x\)\(+9x-18\)\()=\)		Вновь приводим подобные.
\(=-(10x-18)=\)		И раскрываем последнюю скобку. Перед скобкой минус – поэтому все знаки меняются на противоположные.
\(=-10x+18\)		Готово.

Раскрытие скобок — это базовое умение в математике. Без этого умения невозможно иметь оценку выше тройки в 8 и 9 классе. Поэтому рекомендую хорошо разобраться в этой теме.

Задачи на умножение-деление в предалах 100.

1. Ученики 1 класса по заданию учительницы взяли в библиотеке по 2 сказки Пушкина. Сколько всего сказок Пушкина выдал библиотекарь второклассникам, если известно, что во втором классе учится 20 человек?

2. Концертный зал имеет 11 рядов, в каждом ряду по 12 кресел. Сколько зрительских мест в этом зале?

3. Чтобы полить одну грядку с огурцами, бабушке нужно 3 л воды. Сколько литров воды потребуется бабушке, чтобы полить 6 таких грядок?

4. В первой банке 12 литров сока. Во второй — в 2 раза меньше. Сколько сока надо перелить из первой банки во вторую, чтобы в обеих банках стало сока поровну? 

5. У белки в дупле заготовлены на зиму  грибы и орехи. Грибов белка заготовила 86 штук, а орехов всего 4 штуки. Во сколько раз больше белка заготовила грибов, чем орехов?

6. Расстояние от глаз телезрителя до экрана телевизора должна быть в 4 раза больше, чем диагональ экрана. каким должно быть это расстояние, если диагональ экрана равна 36 см?

7. Акула за 10 минут проплывает 1 000 м. Какое расстояние она проплывает за 1 минуту?

8. Заяц за час может пробежать 60 км, а волк на 15 км меньше. какое расстояние может пробежать волк за 1 час?

9. Миша каждый день решал по 5 математических задач. Сколько задач Миша решил за неделю?

10. В магазине в понедельник продали 26 сказок Пушкина, а во вторник в 2 раза меньше. Сколько сказок было всего  продано за 2 дня?

Уважаемые читатели!

Все материалы с сайта можно скачивать абсолютно бесплатно. Все материалы проверены антивирусом и не содержат скрытых скриптов.

Материалы в архиве не помечены водяными знаками!

Если материал нарушает чьи-то авторские права, просьба написать нам по обратной связи, указав авторство материала. Мы обязуемся либо убрать материал, либо указать прямую ссылку на автора.

Сайт пополняется материалами на основе бесплатной работы авторов. Eсли вы хотите отблагодарить их за работу и поддержать наш проект, вы можете перевести любую, не обременительную для вас сумму на счет сайта.
Заранее Вам спасибо!!!

Порядок вычислений в выражениях со скобками

Иногда выражения могут содержать скобки, которые подсказывают порядок выполнения математических действий. В этом случае правило звучит так:

Сначала выполнить действия в скобках, при этом также по порядку слева направо выполняется умножение и деление, затем — сложение и вычитание.

Выражения в скобках рассматриваются как составные части исходного выражения. В них сохраняется уже известный нам порядок выполнения действий.

Рассмотрим порядок выполнения действий на примерах со скобками.

Пример 1. Вычислить: 10 + (8 — 2 * 3) * (12 — 4) : 2.

Как правильно решить пример:

Выражение содержит скобки, поэтому сначала выполним действия в выражениях, которые заключены в эти скобки.

Начнем с первого 8 — 2 * 3. Что сначала, умножение или вычитание? Мы уже знаем правильный ответ: умножение, затем вычитание. Получается так:

8 — 2 * 3 = 8 — 6 = 2.

Переходим ко второму выражению в скобках 12 — 4. Здесь только одно действие – вычитание, выполняем: 12 — 4 = 8.

Подставляем полученные значения в исходное выражение:

10 + (8 — 2 * 3) * (12 — 4) : 2 = 10 + 2 * 8 : 2.

Порядок действий: умножение, деление, и только потом — сложение. Получится:

10 + 2 * 8 : 2 = 10 + 16 : 2 = 10 + 8 = 18.

На этом все действия выполнены.

Ответ: 10 + (8 — 2 * 3) * (12 — 4) : 2 = 18.

Можно встретить выражения, которые содержат скобки в скобках. Для их решения, нужно последовательно применять правило выполнения действий в выражениях со скобками. Удобнее всего начинать выполнение действий с внутренних скобок и продвигаться к внешним. Покажем на примере.

Пример 2. Выполнить действия в выражении: 9 + (5 + 1 + 4 * (2 + 3)).

Как решаем:

Перед нами выражение со скобками. Это значит, что выполнение действий нужно начать с выражения в скобках, то есть, с 5 + 1 + 4 * (2 + 3). Но! Это выражение также содержит скобки, поэтому начнем сначала с действий в них:

2 + 3 = 5.

Подставим найденное значение: 5 + 1 + 4 * 5. В этом выражении сначала выполняем умножение, затем — сложение:

5 + 1 + 4 * 5 = 5 + 1 + 20 = 26.

Исходное значение, после подстановки примет вид 9 + 26, и остается лишь выполнить сложение: 9 + 26 = 35.

Ответ: 9 + (5 + 1 + 4 * (2 + 3)) = 35.

Другие правила раскрытия скобок

Правило раскрытия скобок при делении Если после скобок стоит знак деления — каждое число внутри скобок делится на делитель, который стоит после скобок. Формула раскрытия скобок (a + b) : c = a/c + b/c.

Деление скобки на число предполагает, что необходимо разделить на число все заключенные в скобки слагаемые.

Деление можно предварительно заменить умножением, после чего можно воспользоваться подходящим правилом раскрытия скобок в произведении. Это же правило применимо и при делении скобки на скобку.

Например, нам необходимо раскрыть скобки в выражении (x + 2) : 2/3. Для этого сначала заменим деление умножением на обратное число: 

(x + 2) : 2/3 = (x + 2) * 3/2.

Далее умножим скобку на число:

(x + 2) * 3/2 = x * 3/2 + 2 * 3/2.

Правило раскрытия скобок при умножении: Если перед скобками стоит знак умножения — каждое число, которое стоит внутри скобок, нужно умножить на множитель перед скобками. Формула раскрытия скобок a(b + c) = ab + ac

Пример 1. Раскрыть скобки 5(3 − x)

Как решаем:

В скобке у нас стоят 3 и −x, а перед скобкой — пятерка. Значит, каждый член скобки нужно умножить на 5:

Знак умножения между числом и скобкой в математике не пишут для сокращения размеров записей.

Пример 2. Упростить выражение: 5(x + y) − 2(x − y)

Как решаем: 5(x + y) − 2(x − y) = 5x + 5y − 2x + 2y = 3x + 7y.

Задачи на сложение-вычитание в пределах 20.

1. Поезд прибыл на станцию в 14 часов 19 минут, а должен был согласно расписанию прибыть в 14 часов 14 минут. На сколько минут поезд опоздал?

2. Витя на школьном турнире по шашкам выиграл в 6 партиях, а проиграл в 3. Сколько партий Витя сыграл вничью, если всего он сыграл 12 раз.

3.  Гусь весит 9 кг, а курица на 7 кг меньше. Сколько весят курица и гусь вместе?

4. Бабушка собрала урожай огурцов. Старшей дочери она отвезла 2 ведра огурцов, младшей столько же, а сыну — 3 ведра огурцов. Сколько всего ведер огурцов бабушка отвезла детям?

5. Саша, помогая маме, вымыл 8 тарелок, 4 вилки, 3 кружки и 1 чашку. Сколько всего предметов вымыл Саша?

6. Дима собрал 5 стаканов малины. Бабушка 8 стаканов. На варенье ушло 10 стаканов малины. Сколько стаканов ягоды осталось?

7. В кувшине 4 стакана молока. В бидоне — 8 стаканов молока. За обедом дети выпили 5 стаканов молока. Сколько всего молока осталось? 

8. После обеда Наташа гуляла во дворе 2 часа. Затем она целый час делала домашнее задание. После этого 1 час занималась музыкой и 1 час рисовала. В это время ее позвали ужинать. Во сколько был ужин у Наташи, если обедала она в 2 часа дня.

9. У Ани есть старшая сестра Юля и младший брат Толя. Толе 5 лет. Аня старше его на 3 года. А Юля  старше Толи на 8 лет. На сколько лет Аня младше Юли?

10. На салат пошло 6 огурцов, 5 помидоров и редисок столько, сколько огурцов и помидоров вместе. Сколько всего овощей пошло на салат?

Примеры использования свойств сложения и вычитания

Мы узнали основные свойства сложения и вычитания — осталось попрактиковаться. Чтобы ничего не забыть, используйте эту шпаргалку:

Скачать

Пример 1

Вычислить сумму слагаемых с использованием разных свойств:

а) 4 + 3 + 8

б) 9 + 11 + 2

в) 30 + 0 + 13

Как решаем:

а) 4 + 3 + 8 = (4 + 3) + 8 = 7 + 8 = 15

б) 9 + 11 + 2 = (9 + 2) + 11 = 11 + 11 = 22

в) 30 + 0 + 13 = 30 + 13 = 43

Пример 2

Применить разные свойства при вычислении разности:

а) 25 — 0 — 2

б) 18 — 1 — 4

в) 55 — 55

Как решаем:

а) 25 — 0 — 2 = 25 — 2 = 23

б) 18 — (1 + 4) = 18 — 1 — 4 = 17 — 4 = 13

в) 55 — 55 = 0

Пример 3

Найти значение выражения удобным способом:

а) 11 + 10 + 3 + 9

б) 16 + (4 — 3) + 7

в) 0 + 2 + 4 — 0

Как решаем:

а) 11 + 10 + 3 + 9 = (11 + 10) + (3 + 9) = 21 + 11 = 32

б) 16 — (4 + 3) + 7 = 16 — 4 — 3 + 7 = (16 — 4) — 3 + 7 = 12 — 3 + 7 = 9 + 7 = 16

в) 0 + 2 + 4 — 0 = 2 + 4 = 6

Порядок вычисления простых выражений

Определение 1

В случае выражений без скобок порядок действий определяется однозначно:

1. Все действия выполняются слева направо.
2. В первую очередь мы выполняем деление и умножение, во вторую – вычитание и сложение.

Смысл этих правил легко уяснить. Традиционный порядок записи слева направо определяет основную последовательность вычислений, а необходимость сначала умножить или разделить объясняется самой сутью этих операций.

Возьмем для наглядности несколько задач. Мы использовали только самые простые числовые выражения, чтобы все вычисления можно было провести в уме. Так можно быстрее запомнить нужный порядок и быстро проверить результаты.

Пример 1

Условие: вычислите, сколько будет 7−3+6.

Решение

В нашем выражении скобок нет, умножение и деление также отсутствуют, поэтому выполняем все действия в указанном порядке. Сначала вычитаем три из семи, затем прибавляем к остатку шесть и в итоге получаем десять. Вот запись всего решения:

7−3+6=4+6=10

Ответ: 7−3+6=10.

Пример 2

Условие: в каком порядке нужно выполнять вычисления в выражении 62·83?

Решение

Чтобы дать ответ на этот вопрос, перечитаем правило для выражений без скобок, сформулированное нами до этого. У нас здесь есть только умножение и деление, значит, мы сохраняем записанный порядок вычислений и считаем последовательно слева направо.

Ответ: сначала выполняем деление шести на два, результат умножаем на восемь и получившееся в итоге число делим на три.

Пример 3

Условие: подсчитайте, сколько будет 17−5·63−2+42.

Решение

Сначала определим верный порядок действий, поскольку у нас здесь есть все основные виды арифметических операций – сложение, вычитание, умножение, деление. Первым делом нам надо разделить и умножить. Эти действия не имеют приоритета друг перед другом, поэтому выполняем их в написанном порядке справа налево. То есть 5 надо умножить на 6 и получить 30, потом 30 разделить на 3 и получить 10. После этого делим 4 на 2, это 2. Подставим найденные значения в исходное выражение:

17−5·63−2+42=17−10−2+2

Здесь уже нет ни деления, ни умножения, поэтому делаем оставшиеся вычисления по порядку и получаем ответ:

17−10−2+2=7−2+2=5+2=7

Ответ: 17−5·63−2+42=7.

Пока порядок выполнения действий не заучен твердо, можно ставить над знаками арифметических действий цифры, означающие порядок вычисления. Например, для задачи выше мы могли бы записать так:

.

Если у нас есть буквенные выражения, то с ними мы поступаем точно так же: сначала умножаем и делим, затем складываем и вычитаем.

Порядок вычислений в выражениях со скобками

Скобки сами по себе являются знаком, который сообщает нам нужный порядок выполнения действий. В таком случае нужное правило можно записать так:

Определение 3

Если в выражении есть скобки, то первым делом выполняется действие в них, после чего мы умножаем и делим, а затем складываем и вычитаем по направлению слева направо.

Что касается самого выражения в скобках, его можно рассматривать в качестве составной части основного выражения. При подсчете значения выражения в скобках мы сохраняем все тот же известный нам порядок действий. Проиллюстрируем нашу мысль примером.

Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!

Описать задание

Пример 4

Условие: вычислите, сколько будет 5+(7−2·3)·(6−4)2.

Решение

В данном выражении есть скобки, поэтому начнем с них. Первым делом вычислим, сколько будет 7−2·3. Здесь нам надо умножить 2 на 3 и вычесть результат из 7:

7−2·3=7−6=1

Считаем результат во вторых скобках. Там у нас всего одно действие: 6−4=2.

Теперь нам нужно подставить получившиеся значения в первоначальное выражение:

5+(7−2·3)·(6−4)2=5+1·22

Начнем с умножения и деления, потом выполним вычитание и получим:

5+1·22=5+22=5+1=6

На этом вычисления можно закончить.

Ответ: 5+(7−2·3)·(6−4)2=6.

Не пугайтесь, если в условии у нас содержится выражение, в котором одни скобки заключают в себе другие. Нам надо только применять правило выше последовательно по отношению ко всем выражениям в скобках. Возьмем такую задачу.

Пример 5

Условие: вычислите, сколько будет 4+(3+1+4·(2+3)).

Решение

У нас есть скобки в скобках. Начинаем с 3+1+4·(2+3), а именно с 2+3. Это будет 5. Значение надо будет подставить в выражение и подсчитать, что 3+1+4·5. Мы помним, что сначала надо умножить, а потом сложить: 3+1+4·5=3+1+20=24. Подставив найденные значения в исходное выражение, вычислим ответ: 4+24=28.

Ответ: 4+(3+1+4·(2+3))=28.

Иначе говоря, при вычислении значения выражения, включающего скобки в скобках, мы начинаем с внутренних скобок и продвигаемся к внешним.

Допустим, нам надо найти, сколько будет (4+(4+(4−62))−1)−1. Начинаем с выражения во внутренних скобках. Поскольку 4−62=4−3=1, исходное выражение можно записать как (4+(4+1)−1)−1. Снова обращаемся к внутренним скобкам:  4+1=5. Мы пришли к выражению (4+5−1)−1. Считаем 4+5−1=8 и в итоге получаем разность 8-1, результатом которой будет 7.

Свойства вычитания

Вычитание— это арифметическое действие, в котором отнимают меньшее число от большего.

Для записи вычитания используется знак «-» (минус), который ставится между уменьшаемым и вычитаемым.

Уменьшаемое — это число, из которого вычитают.

Вычитаемое — это число, которое вычитают.

Разность — это число, которое получается в результате вычитания.

Рассмотрим пример 9 — 4 = 5, в котором:

9 — это уменьшаемое,

4 — вычитаемое,

5 — разность.

При этом саму запись (9 — 4) тоже можно назвать разностью.

Свойства вычитания Свойство нуля при вычитании Если из числа вычесть нуль, получится само число. a — 0 = a Если из числа вычесть само число, то получится нуль. a — a = 0 Свойство вычитания суммы из числа Чтобы вычесть сумму из числа, можно вычесть из этого числа одно слагаемое, из полученной разности — второе слагаемое. a — (b + c) = a — b — c Свойство вычитания числа из суммы Чтобы вычесть число из суммы, можно вычесть его из одного слагаемого, а к результату прибавить оставшееся слагаемое. (a + b) — c = (a — c) + b (если a > c или а = с) (a + b) — c = (b — c) + a (если b > c или b = с)

На заметку!
Есть случаи, когда скобки не имеют значения при вычитании, и их можно опустить. Например: (a — b) — c = a — b — c.

Презентация 2 класса по предмету «Математика» на тему: «Урок математики Тема: «Порядок действий.Скобки» 2 класс Лобова Ольга Викторовна МОУ СОШ с.Васильевка.». Скачать бесплатно и без регистрации. — Транскрипт:

2

Урок математики Тема: «Порядок действий.Скобки» 2 класс Лобова Ольга Викторовна МОУ СОШ с.Васильевка

3

Скобки! Математический знак. Математический знак. Ставятся, упорядочивают, указывают. Ставятся, упорядочивают, указывают. Они сторожа счета. Они сторожа счета. Порядок действий! Порядок действий!

4

Цель: Создать условия для формирования умений применять знания правила порядка выполнения действий в выражениях со скобками в различных ситуациях Создать условия для формирования умений применять знания правила порядка выполнения действий в выражениях со скобками в различных ситуациях

5

Задачи: формировать знания о правилах порядка действий в выражениях со скобками;формировать знания о правилах порядка действий в выражениях со скобками; способствовать развитию умений и навыков решения примеров со скобками; текстовых задачспособствовать развитию умений и навыков решения примеров со скобками; текстовых задач воспитывать у учащихся нравственные качества (организованность и доброжелательность).воспитывать у учащихся нравственные качества (организованность и доброжелательность).

6

Напомните условие задачи по краткой записи: ____________?мин________ ___I_______II_______III___ 10мин. 20мин 10мин 10мин. 20мин 10мин 10+20=30 (мин) 10+30=40 (мин) 10+(10+20)=40 (мин) Ответ: 40 минут тратит папа на дорогу

11

Логика Задача для ума Задача для ума В чудо – мешочке находятся 3 белых и 3 синих шарика. Сколько нужно вынуть шариков из мешочка, чтобы заранее утверждать, что хотя бы 1 будет белым? В чудо – мешочке находятся 3 белых и 3 синих шарика. Сколько нужно вынуть шариков из мешочка, чтобы заранее утверждать, что хотя бы 1 будет белым?

13

малирн +

14

Проблема! 8 – = = 1 1) 2)

15

-Сравните выражения и результаты. Что заметили? — Почему? Как выполняли действия? — Как нам изменить выражения, ведь судя по результату они не равны? Нам необходимо как-то обозначить в записи порядок действий. Предложите свои способы обозначения порядка действий. Может быть надо ограничить, отделить действия одно от другого? 8 –/ 3 + 4/= 1

16

Принято в математике обозначать очерёдность действий с помощью скобок. ( ) Действие которое написано в скобках выполняется первым. 8 — (3 + 4 ) = 1

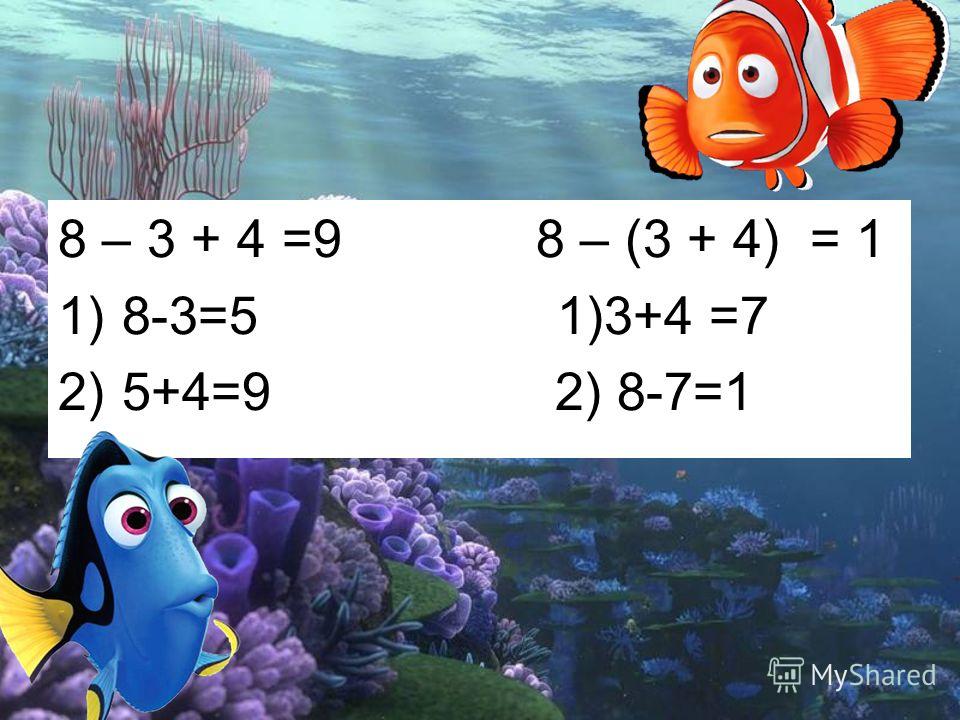
17

8 – =9 8 – (3 + 4) = 1 1)8-3=5 1)3+4 =7 2)5+4=9 2) 8-7=1

18

Составьте алгоритм действий для решения примеров без скобок и примеров со скобками. Помните, что действие записанное в скобках выполняется первым

19

Алгоритм выполнения действий 1. В скобках 2. По порядку слева направо

23

Задача 7 (стр 23) ____________?____________ ___I_______II_______III___ 39р. ?на 12р. 39р. ?на 12р.

24

Задача 7 (стр 23) ____________?____________ ___I_______II_______III___ 39р. ?на 12р. 39р. ?на 12р. I способ I способ 1)39-12 =27(р.) во втором букете 1)39-12 =27(р.) во втором букете 2)39+4=43(р.) в третьем букете 2)39+4=43(р.) в третьем букете 3) =109(р.) 3) =109(р.)

25

Задача 7 (стр 23) I способ 1)39-12 =27(р.) во втором букете 1)39-12 =27(р.) во втором букете 2)39+4=43(р.) в третьем букете 2)39+4=43(р.) в третьем букете 3) =109(р.) 3) =109(р.) II способ 39+ (39-12)+(39+4)=109(р.) Ответ: 109 ромашек в трех букетах

29

1.Укажите, какое действие будете выполнять первым 8-(3+4) а) + б)- 2. Укажите, какое действие вы будете выполнять последним а) + б) —

30

3. Укажите выражение со значением 40 а) (21+13)-11 б) 75-(20+15) в) (61+20) Расставьте порядок действий в выражениях (78+12) — (12-9) ; а — (в + с)

31

Вспомните тему урока. Что узнали нового? Назовите порядок действий в выражениях без скобок. В выражениях, содержащих скобки. Подведем итог. Чтобы правильно решить выражения со скобками мы должны соблюдать порядок действий. Помнить, что первыми выполняются действия записанные в скобках.

Математика. 2 класс. И семестр разработки уроков

ТАБЛИЦЫ СЛОЖЕНИЯ И ВЫЧИТАНИЯ ЧИСЕЛ. ЗАДАЧИ НА ДВА ДЕЙСТВИЯ. ВЫРАЖЕНИЯ СО СКОБКАМИ

Урок 27. ВЫРАЖЕНИЯ СО СКОБКАМИ. ПОРЯДОК ВЫПОЛНЕНИЯ ДЕЙСТВИЙ В ВЫРАЖЕНИЯХ, СОДЕРЖАЩИХ СКОБКИ. ЗАДАЧИ НА ДВА ДЕЙСТВИЯ

Цель: ознакомить учащихся с порядком выполнения действий в выражениях, содержащих скобки; развивать мышление, внимание; воспитывать интерес к предмету, бережное отношение друг к другу. Задача 216

Задача 216

— Прочитайте выражения в порядке возрастания ответов.

Задание 217

— Прочитайте решение задачи двумя способами.

— Установите закономерность и запишите числа, вставляя пропущенные.

2; 3; 6; 7; 10; 11; ?; ?; ?; ?.

III. СООБЩЕНИЕ ТЕМЫ И ЦЕЛИ УРОКА

— Сегодня на уроке мы ознакомимся с порядком выполнения действий в выражениях, содержащих скобки.

IV. ИЗУЧЕНИЕ НОВОГО МАТЕРИАЛА

Задача 219. Коллективное обработки материала

— Иногда действия в выражениях можно выполнять не по порядку. Действие, которое выполняется первым, берется в скобки: ( ). Эти значки — не простые, а волшебные. Их применяют, чтобы изменить порядок выполнения действий в выражениях.

Если в числовом выражении есть скобки, то первой всегда выполняют то действие, которое в скобках.

17 — (4 + 5) = 17 — 9 = 8

Выражение читают так: «От 17 отнять сумму чисел 4 и 5».

Задача 220. Коллективное обработки материала

В свитке было 15 м ткани. Первый покупатель приобрел 5 м ткани, а второй — 3 м. Сколько метров ткани осталось в свитки?

— Чтобы узнать, сколько метров ткани осталось в свитки, продавец действовал так: вычислил, сколько всего метров ткани продано, а потом добытое число отнял от 15.

15 — (5 + 3) = 7 (г)

Скобки означают, что сначала нужно найти сумму, а затем выполнить действие вычитания.

Вывод. В выражениях со скобками первой выполняют действие над числами, записанными в скобках.

Задача 221

Ученики «цепочкой» читают и записывают выражения. Один ученик решает у доски, остальные — в тетрадях.

• От числа 12 вычесть сумму чисел 7 и 2.

• К числу 8 прибавить разность чисел 13 и 6.

Задача 222

Во время повторения условия один ученик чертит схему и объясняет решение. После этого ученики самостоятельно записывают решение. Проверяют ответ, решив задачу другим способом.

Задача 223. Коллективное ознакомление с содержанием задачи, ее анализ Один ученик записывает условие и решает задачу.

— Как изменится решение задачи, если у другой белки на 2 орехи меньше?

Задача 224*. Самостоятельная работа

Ученики записывают двоцифрові числа, оканчивающиеся цифрой 5, можно записать с помощью цифр 5; 6; 7; 8. (55; 65; 75; 85)

2. Физкультминутка

V. ОБОБЩЕНИЕ И СИСТЕМАТИЗАЦИЯ ЗНАНИЙ

1. Вычисление значений выражений

— Прочитайте выражения и вычислите по образцу:

29 — (4 + 5) = 29 — 9 = 20

5 + (18 — 9)

21 — (40 — 20)

94 — (54 + 40)

15 + (19 — 16)

2. Игра «Выбери и реши»

— Решите примеры, в которых вычитаемое равно 7; слагаемое равно 7.

3. Офтальмологическая пауза

4. Решение логических задач

• У трех братьев по одной сестре. Сколько всего детей в семье? (4)

• Гусь имеет массу 3 кг. Какова будет ее масса, если она станет на одну ногу? (3 кг)

VИ. ПОДВЕДЕНИЕ ИТОГОВ. РЕФЛЕКСИЯ

— Что нового узнали на уроке?

— Какое правило о порядке действий запомнили?

VII. ДОМАШНЕЕ ЗАДАНИЕ

С. 40, задание 225; 226.

Назад

Вперед

Свойства сложения

Сложение — это арифметическое действие, в котором единицы двух чисел объединяются в одно новое число

Для записи сложения используют знак «+» (плюс), который ставят между слагаемыми.

Слагаемые — это числа, единицы которых складываются.

Сумма — это число, которое получается в результате сложения.

Рассмотрим пример 2 + 5 = 7, в котором:

• 2 — это первое слагаемое,
• 5 — второе слагаемое,
• 7 — это сумма.

При этом саму запись (2 + 5) можно тоже назвать суммой.

Сложение двух чисел можно проверить вычитанием. Для этого вычитаем из суммы одно из слагаемых. Если разность окажется равной другому слагаемому — сложение выполнено верно.

Впервые мы сталкиваемся со свойствами сложения во 2 классе. С каждым годом задания усложняются, и появляются новые правила и законы. Рассмотрим свойства сложения для 4 класса.

Свойства сложения Переместительное свойство сложения От перестановки мест слагаемых сумма не меняется. a + b = b + a Сочетательное свойство сложения Чтобы к сумме двух чисел прибавить третье нужно к первому числу прибавить сумму второго и третьего числа. (a + b) + c = a + (b + c) Свойство нуля при сложении Если к числу прибавить нуль, получится само число. a + 0 = 0 + a = a

На заметку!
При сложении нескольких чисел, их можно объединять в группы и переставлять в любом порядке. Например: a + b + с = (a + b) + c = a + (b + c).