Вычитание столбиком

Как объяснить деление столбиком

Сначала стоит доходчиво объяснить, что такое деление на простом примере. Суть математического действия — разложить число поровну. В 3-м классе дети хорошо учатся на доступных примерах: раздают кусочки торта гостям, рассаживают кукол по 2 машинам.

Когда малыш усвоит суть деления, покажите его запись на листке. Используйте уже знакомые задания с простыми числами:

• Сначала запишите задачу обычным способом: 250:2=?
• Каждому числу дайте название: 250 — делимое, 2 — делитель, результат после знака равно — частное.
• Затем сделайте сокращенную запись столбиком (уголком):

• Рассуждайте вместе так: сначала найдем неполное частное. Для этого нам потребуется сравнивать первое неполное делимое и делитель. Это будет 2, так как оно не меньше делителя, а вернее, равно ему. В этом числе помещается один делитель, значит, в частное записываем цифру 1 и умножаем ее на 2. Заносим полученный результат под делимым. Отнимаем 2-2. Получится ноль, поэтому сносим следующее число и опять подыскиваем частное. Совершаем математическое действие до тех пор, пока не получится ноль.
• После получения окончательного результат сделайте проверку с помощью умножения: 125х2=250.

Во время объяснения правил деления в столбик желательно научить третьеклассника рассуждать в процессе вычисления вслух, выполнять действия на черновике.

Сначала проговаривайте алгоритм вместе, потом только слушайте ученика и помогайте исправить ошибки.

Алгоритм деления столбиком

1. Запишем числа вместе с символом деления столбиком. Теперь смотрим на первую слева цифру в записи делимого. Возможны два случая: число, определяемое этой цифрой, больше, чем делитель, и наоборот. В первом случае мы работаем с этим числом, во втором — дополнительно берем следующую цифру в записи делимого и работаем с соответствующим двузначным числом. Согласно с этим пунктом, выделим в записе примера число, с которым будем работать первоначально. Это число — 14, так как первая цифра делимого 1 меньше, чем делитель 4.

2. Определяем, сколько раз числитель содержится полученном числе. Обозначим это число как x=14 . Последовательно умножаем делитель 4 на каждый член ряда натуральных чисел ℕ, включая нуль : , 1, 2, 3 и так далее. Делаем это, пока не получим в результате x или число, большее чем x. Когда в результате умножения получается число 14, записываем его под выделенным числом по правилам записи вычитания в столбик. Множитель, на который умножался делитель, записываем под делителем. Если в результате умножения получается число, большее чем x, то под выделенным числом записываем число, полученное на предпоследнем шаге, а на место неполного частного (под делителем) пишем множитель, на который на предпоследнем шаге проводилось умножение.

В соответствии с алгоритмом имеем:

4·=<14; 4·1=4<14; 4·2=8<14; 4·3=12<14; 4·4=16>14.

Под выделенным числом записываем число 12, полученное на предпоследнем шаге. На место частного записываем множитель 3.

3. Столбиком вычитаем  из 14 12 , результат записываем под горизонтальной чертой. По аналогии с первым пунктом сравниваем полученное число с делителем. 

4. Число 2 меньше числа 4, поэтому записываем под горизонтальной чертой после двойки цифру,расположенную в следующем разряде делимого. Если же в делимом более нет цифр, то на этом операция деления заканчивается. В нашем примере после полученного в предыдущем пункте числа 2 записываем следующую цифру делимого — . В итоге отмечаем новое рабочее число — 20.

Важно!

Пункты 2-4 повторяются циклически до окончания операции деления натуральных чисел столбиком.

2. Снова посчитаем, сколько делителей содержится в числе 20. Умножая 4 на , 1, 2, 3..  получаем:

4·5=20

Так как мы получили в результе число, равное 20 , записываем его под отмеченным числом, а на месте частного, в следубщем разряде, записываем 5 — множитель, на который проводилось умножение. 

3. Проводим вычитание столбиком. Так как числа равны, получаем в результате число ноль: 20-20=.

4. Мы не будем записывать число ноль, так как данный этап — еще не окончание деления. Просто запомним место, куда мы могли его записать и запишем рядом число из следующего разряда делимого. В нашем случае — число 2.

Принимаем это число за рабочее и снова выполняем пункты  алгоритма.

2. Умножаем делитель на , 1, 2, 3.. и сравниваем результат с отмеченным числом.

4·=<2; 4·1=4>2

Соответственно, под отмеченным числом записываем число , и под делителем в следующий разряд частного также записываем .

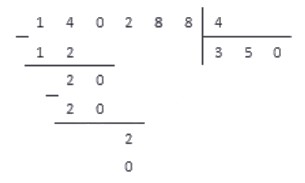
3. Выполняем операцию вычитания  и под чертой записываем результат.

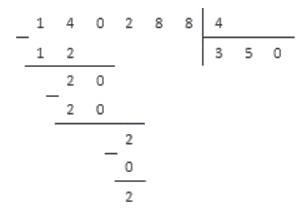
4. Справа под чертой добавляем цифру 8, так как это следующая цифра делимого числа.

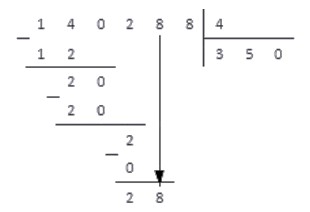
Таким образом, получаем новое работчее число — 28. Снова повторяем пункты алгоритма.

Проделав все по правилам, получаем результат:

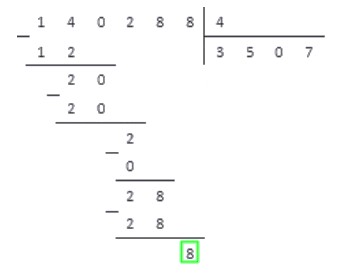
Переносим под черту вниз последнюю цифру делимого — 8. В последний раз повторяем пункты алгоритма 2-4 и получаем:

В самой нижней строчке записываем число . Это число записывается только на последнем этапе деления, когда операция завершена.

Таким образом, результатом деления числа 140228 на 4 является число 35072. Данный пример разобран очень подробно, и при решении практических заданий расписывать все действия столь досканально не нужно.

Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!

Описать задание

Приведем другие примеры деления чисел в столбик и примеры записи решений.

Пример 1. Деление натуральных чисел в столбик

Разделим натуральное число 7136 на натуральное число 9.

Запишем:

После второго, третьего и четвертого шага алгоритма запись примет вид:

Повторим цикл:

Последний проход, и поучаем результат:

Ответ: Неполное неполное частное чисел 7136 и 9 равно 792, а остаток равен 8.

При решении практических примеров в иделе вообще не использовать пояснения в виде словесных комментариев.

Пример 2. Деление натуральных чисел в столбик

Разделим число 7042035 на 7.

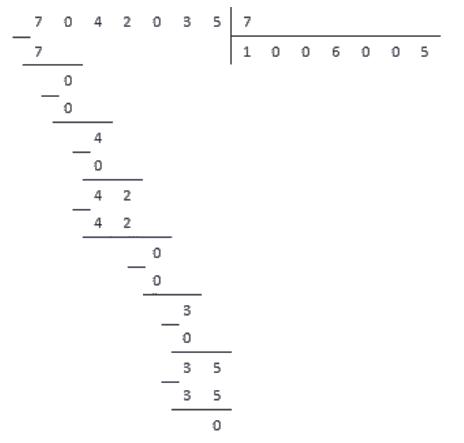
Ответ: 1006005

Правила вычитания в столбик

Чтобы найти разность двух и более чисел с любым количеством разрядов можно выполнить вычитание в столбик. Для этого:

1. Записываем уменьшаемое в самой верхней строчке.
2. Под ним записываем первое вычитаемое – таким образом, чтобы одинаковые разряды обоих чисел находились друг под другом (десятки под десятками, сотни под сотнями и т.д.)
3. Таким же способом дописываем другие вычитаемые, если они есть. В результате образуются столбцы с разными разрядами.
4. Под записанными числами чертим горизонтальную линию, которая будет отделять уменьшаемое и вычитаемые от разности.
5. Переходим к вычитанию цифр. Эта процедура выполняется справа налево, отдельно для каждого столбца, а результат пишем под чертой в том же самом столбце. Здесь есть пара нюансов:
   • Если из цифры в уменьшаемом нельзя отнять цифры в вычитаемых, значит занимаем десяток у более старшего разряда, и затем обязательно учитываем это в дальнейших действиях (см. Пример 2).
   • Если в уменьшаемом стоит ноль, это автоматически означает, что для выполнения вычитания нужно занять у следующего разряда (см. Пример 3).
   • Иногда в результате “займа” в более старшем разряде может не остаться цифр (см. Пример 4).
   • В редких случаях, когда вычитаемых много, требуется занять не один, а сразу два и более десятка (см. Пример 5).

Решение задач с единицами площади

Ребята, взрослые люди часто испытывают досаду, занимаясь ремонтом дома или квартиры. Почему? Знакома ситуация, когда чуть-чуть не хватило краски или обоев? Нужно срочно бежать в магазин, чтобы купить недостающие материалы. Можно ли этого избежать? Конечно, можно! Главное, правильно выполнить расчеты. Например, правильно измерить площадь пола под покраску или площадь стен под обои.

Задача

В комнате длиной 7 м и шириной 8 м укладывают на пол ламинат квадратами 50х50 см. Сколько штук ламината потребуется для этой комнаты?

Подсказка. Вычислите площадь комнаты и площадь одного квадрата ламината. Одинаковые ли единицы площади вы использовали? Выразите квадратные метры в квадратных сантиметрах.

Решите задачу самостоятельно.

Проверь себя.

S пола = 7 ∙ 8 = 56 (м²)

S лам. = 50 ∙50 = 2 500 (см²)

1 м² = 10 000 см²

10 000 : 2 500 = 4 (шт.) – ламината в 1 м².

56 ∙ 4 = 224 (шт.) – ламината потребуется.

Ответ: 224 штук ламината.

Задача

Для покраски пола комнаты площадью 35 м² купили 3 кг краски. Хватит ли этой краски, если на 1 м² пола расходуется 100 г краски.

Выразим 3 кг в граммах.

1 кг = 1 000 г

3 кг = 3 000 г

35 ∙ 100 = 3 500 (г) – краски потребуется.

3 500 – 3000 = 500 (г) – краски не хватит для покраски пола.

Ответ: 500 г краски не хватит.

Решите аналогичную задачу самостоятельно и проверьте по образцу.

Задача

Стены комнаты решили оклеить обоями. Площадь поверхности составляет 80 м². На одной стене есть окно – 3 м², а на другой – дверь занимает 4 м². Хватит ли 7 рулонов обоев, если в одном рулоне 10 м² обоев.

Проверь себя.

3 + 4 = 7 (м²) – занимают окно и дверь.

80 – 7 = 73 (м²) – нужно оклеить обоями.

7 ∙ 10 = 70 (м²) – в семи рулонах.

73 – 70  = 3 (м²) – обоев не хватит.

Ответ: не хватит 3 м².

Ребята, на уроке мы учились делить на трехзначное число без остатка и с остатком, решали сложные задачи с единицами площади. А теперь настало время подвести итоги! Устроим небольшое соревнование на звание «Знатока математики».

Решите примеры за одну минуту!

(12 543 – 3 890 + 15 498) ∙ 69 ∙ 0 ∙594 =

640 ∙5 ∙0 +640 : 1 – 630 =

? + 150 – 240 – 10 + 26 = 526

Проверь себя.

0, 10, 600.

Кому удалось справиться с заданием за одну минуту, может смело назвать себя большим молодцом!

В первом и втором выражениях самые наблюдательные заметили умножение на нуль (можно не вычислять все выражение, а ∙ 0 = 0).

В третьем выражении первое число можно быстро найти, вычисляя с конца обратным действием: 526 – 26 + 10 + 240 – 150 = 600

Правила деления в столбик

Без остатка

Чтобы найти частное от деления одного числа на другое (с любым количеством разрядов) можно выполнить это арифметическое действие в столбик.

Рассмотрим правила деления на практическом примере для лучшего понимания. Допустим, нам нужно трехзначное число разделить на однозначное, к примеру 256 на 8. Вот, что мы делаем:

1. Пишем делимое (256), затем немного отступаем от него и в этой же строке дописываем делитель (8). Затем между этими числами дорисовываем уголок. Результат будем записывать под делителем.

2. В делимом слева направо отсчитываем минимально необходимое количество разрядов таким образом, чтобы полученное из содержащихся в них цифр новое число было больше, чем делитель. В нашем случае числа 2 недостаточно, поэтому к нему добавляем 5 и в итоге получаем 25.

Примечание: Если крайняя левая цифра делимого больше делителя, добавлять к нему цифру следующего разряда не нужно, и мы сразу приступаем к следующему шагу.

3. Определяем, сколько целых раз наш делитель содержится в полученном из цифр делимого числе (25). В нашем случае – три раза. Пишем цифру 3 в отведенном для этого месте, затем умножаем ее на делитель (3 ⋅ 8). Получившееся число (24) отнимаем из 25 и остается единица

Важно, чтобы результат вычитания (остаток) обязательно был меньше делителя, иначе мы неправильно выполнили вычисления

Примечание: Правила и примеры вычитания чисел столбиком приведены в отдельной публикации.

4. К остатку (1) добавляем следующую цифру делимого (6), чтобы получить новое число, которое снова больше, чем делитель.

Примечание: Если при добавлении следующей цифры образовавшееся новое число все еще меньше делителя, берем еще одну цифру справа (если есть такая возможность), при этом в частном пишем ноль. В противном случае, получается деление с остатком, которое мы рассмотрим далее.

5. В числе 16 содержится ровно два раза по восемь (2 ⋅ 8), следовательно, пишем 2 в частном, затем выполняем вычитание (16 – 16) и получаем остаток, равный нулю.

На этом деление столбиком числа 256 на 8 успешно выполнено, и частное равно 32.

С остатком

В целом, алгоритм действий аналогичен вышеописанному. Разница лишь в том, что при последнем вычитании остается неделимой остаток, к которому больше нечего дописывать из делимого, т.к. все его разряды уже были использованы. Остаток обычно записывается справа от результата в скобках.

Например, остаток от деления 112 на 5 равняется двум. То есть 112 : 5 = 22 (2).

Пояснение: в результате вычитания 10 из 12 получается 2, но к нему больше нечего дописать из делимого.

Принцип деления для детей

Дальше приступают к формированию самого понимания, что деление – это процесс разделения чего-нибудь на одинаковые части. Проще всего обучить ребенка такому математическому действию – попросить разделить небольшое количество предметов между ним и членами семьи. Используя игровой подход, ему легче уловить суть самого процесса деления.

Так, например, просят разделить апельсин на дольки между ним и членами семьи, чтобы у всех было поровну. Сначала ребенок будет перекладывать по одной штучке. Потом нужно предложить ему подсчитать, сколько долек было изначально, и какое количество досталось каждому.

Надо показать ребенку, что уметь разделить предметы – значит разложить их таким образом, чтобы все получили поровну независимо от количества участников. При этом объясняют, что не всегда их можно разделить на одинаковые части. Приводят пример. Если 10 яблок разделить между папой, мамой и бабушкой, то каждый получит по 3 штуки, а 1 останется.

Чтобы процесс обучения давался ребенку более легко, можно использовать наглядный материал. Используйте счетные палочки, раскладывая их в отдельные «кучки», имитируя деление палочек на несколько равных частей. Можно использовать орешки, семечки, карандаши. Обязательное условие – учитесь играя.

После того, как ребенок усвоил саму суть принципа деления, надо начинать изучать математическую запись этой операции. Объясняют, что деление – операция противоположная умножению. Демонстрируют это с помощью таблицы умножения.

Например, 3х2=6. Надо повторить, что произведение данных чисел равно результату умножения. Потом показать, что операция деления, противоположная умножению и все это показать ребенку. Делят наше произведение «6» на множитель «3», и в результате будет другой множитель.

Задача родителей – объяснить юному дарованию таблицу умножения «наизнанку»

Очень важно, чтобы ребенок ее хорошо усвоил. Это знание будет просто необходимо для изучения деления в столбик

Методика деления в столбик

Существует определенный алгоритм для деления в столбик. Изучается он в начальных классах средних образовательных школ. Методику можно применять не только для положительных, но и отрицательных значений. При этом нужно учитывать знак:

1. Деление отрицательной величины на отрицательную — положительное значение.
2. При делении положительного на отрицательное или наоборот — отрицательная величина.

Алгоритм без остатка

Методика применяется в том случае, когда делимое является не простым числом, а содержит множители. Кроме того, при его делении на делитель, не соответствующий одному из признаков деления. Например, 33 делится на 2 с остатком. Однако, когда делитель равен 3, то последнего нет.

Для применения алгоритма нужно наглядно разобрать следующий пример: требуется разделить 78 на 2. Методика выполнения этой операции имеет следующий вид:

1. Записать делимое с левой стороны, а делитель — справа.
2. По карточке простых чисел или при помощи ручного метода необходимо определить принадлежность делимого к простым значениям (78 делится на 2, поскольку заканчивается на четную цифру 8).
3. Разделить две значения вертикальной чертой.
4. Выделить I неполное делимое: 7.
5. По таблице умножения подобрать ближайшее целое (3). При произведении его на делитель должно получиться значение, которое меньше первого неполного делимого (3 * 2 = 6 < 7). Если записать 4, то 4 * 2 = 8 > 7 (вариант не подходит).
6. Записать число, полученное при умножении делителя на подобранное значение, под I неполным делимым. Произвести операцию вычитания (7 — 6 = 1).
7. Результат вычитания (1), который называется остатком, не делится на 2. Следовательно, нужно дописать II неполное делимое (18). Если по какой-то причине, результат делится на делитель, то подобранное значение является неверным.
8. Значение 18 делится на 2, т. е. 18/2 = 9.
9. Результат деления 78 на 2 равен 39.

Операция с остатком

Не во всех случаях результат деления двух чисел является целой величиной. В школьной программе встречается группа примеров, в которых требуется найти остаток, полученный при выполнении операции деления 2 значений (77/3). Алгоритм похож на предыдущий, но имеются некоторые особенности:

1. Два числа записываются, как и в предыдущем случае.
2. Принадлежность к множеству простых чисел не проверяется.
3. Выделить I неполное делимое: 7.
4. Подобрать ближайшее целое число, записав его в результат: 2.
5. Выполнить проверку: 3 * 2 = 6 < 7 (значение подходит).
6. Записать 6 под 7, а затем выполнить операцию вычитания: 7 — 6 = 1. Остаток меньше 3, следовательно, число подобрано правильно.
7. Выполнить подбор множителя для 17: целочисленного значения нет. Следовательно, нужно подобрать ближайшее целое: 5.
8. Произвести проверку: 3 * 5 = 15 < 17.
9. Записать 5 в результат и определить остаток: 17 — 15 = 2.
10. Результат деления 77 на 3 эквивалентен: 25 с остатком 2.

Таким образом, для выполнения операции деления двузначного числа на однозначное нужно знать признаки делимости величин, а также основные алгоритмы деления с остатком и без него.

Деление столбиком если делимое меньше делителя

Как разделить столбиком, если делитель больше делимого!

Пример №1.(В1.)

Предположим, что вам нужно разделить 4 на 5.

Располагаем стандартно наши числа слева делимое, справа делитель.

Ясно, что делитель больше делимого 5 > 4.

Поэтому, рядом с число 4 пишем ноль(выделено зеленым) и одновременно, этот же ноль записываем под делителем и добавляем точку.

Проверяем 40 делится на 5 — делится. 40 : 5 = 8, восемь записываем под черту, 40 пишем под делимым.

Отнимаем 40 — 40 = 0.

Итого получаем, что если разделить 4 на 5, то получим 0.8 — ноль целых восемь десятых.

Пример №2.(В2.)

Разберем второй пример :

Предположим, что нам нужно разделить 4 на 50.

Располагаем стандарно, наши числа для деления столбиком.

Ясно, что 4 меньше 50.

Пишем ноль рядом с 4, и одновременно ноль пишем под чертой ставим точку.

Проверяем, делится ли 40 на 50 — нет! Значит, добавляем еще один ноль. И его же добавляем после точки.

Далее аналогичные действия, что производили в первом варианте.

Деление на двузначное число с остатком

Действует ли при делении с остатком какой-либо другой алгоритм? Нет! При делении с остатком рассуждают точно так же, как и при делении без остатка.

Ребята, какое правило нужно знать и обязательно проверять при делении с остатком?

А теперь решите самостоятельно примеры на деление с остатком. Не забывайте сравнивать остаток с делителем, сделайте проверку.

272 : 98    495 : 46    385 : 65   321 : 47

Проверь себя.

Ребята, в каком примере вы встретили затруднение? Рассмотрим вместе пример

495 : 46

Почему в частном появился 0 (нуль)?

Первое неполное делимое 49. Делим на 46. Берем по 1. Остаток 3 меньше делителя 46. Делим верно. Сносим следующую цифру 5.

35 делим на  46. Берем по 0 (35 меньше, чем 46).  Остаток 35 меньше делителя, разделили верно. Сделаем проверку, убедимся в правильности вычислений.

Уметь делить с остатком – полезный навык, который не раз поможет вам в решении практических задач. Например, для постройки одинаковых башен у вас имеется 430 деталей лего-конструктора. Сколько башен можно построить, если на каждую нужно 35 деталей? Останутся ли лишние детали?

Давайте вместе решим эту задачу.

430 разделим на 35. Сделаем это столбиком (уголком).

Мы видим, что при делении получился остаток 10. Делаем вывод: из 430 деталей лего-конструктора можно сделать 12 одинаковых башен и еще 10 деталей останется.

Разделить можно на черновике, а решение в тетради записать в строчку.

430 : 35 = 12 (ост.10) – башен можно сделать.

Ответ: 12 башен и 10 деталей останется.

Если вы хорошо умеете делить с остатком, решение можно сразу записать в тетрадь:

Решите самостоятельно практическую задачу.

Задача

Ребята 4 класса изготовили для первоклассников 126 закладок в учебники. Сколько закладок достанется каждому первокласснику, если в первом классе 25 учеников? Останутся ли лишние закладки?

Проверь себя.

Пример выполнения деления в столбик

Деление с использованием конкретного примера самая эффективная и распространённая методика в обучении детей делению в столбик. Ученику предлагается разделить трехзначное число, допустим «945» на однозначное число «5» в столбик. В качестве примера лучше брать трехзначное и выше по значению число, чтобы сразу ликвидировать у ребенка страх перед большим числом, которое предстоит делить в столбик.

1 Этап. Школьник должен безошибочно назвать компоненты выражения, которое ему предстоит выполнить. Если все пояснения им усвоены, то ему не составит труда определить «945» как делимое, «5» как делитель, а результат, который будет извлечен после процедуры деления как частное. Чем собственно говоря он сейчас и должен заняться.

2 Этап. Ученика попросить сначала записать в ряд 945 и 5, а затем поделить их с помощью «уголка».

3 Этап. Ребенку предлагается рассмотреть делимое двигаясь слева направо по этому числу и определяя наименьшее число, которое будет больше делителя. Школьник выбирает между числами:9, 94 и 945, соответственно, наименьшим будет число 9. Затем ему надо ответить на вопрос, какое количество раз число 5 поместиться в числе 9? Правильным ответом ученика будет, — один. Соответственно 1 записывается под чертой, и оно станет первой цифрой искомого частного.

4 Этап. Начинается формирование столбика деления. Ребенок должен будет умножить получение число 1 на 5, получив соответственно 5. Результат этой операции записывается под первой цифрой делимого, из числа 9 вычитается 5. Ребенок должен назвать результат и записать его – это число 4.

На этом этапе принципиально важным станет пояснения, что результат вычитания всегда должен получаться меньше делителя, если это не так, значит допущена ошибка при определении какое количество раз число 5 может «поместиться» в числе 9. Естественным будет то, что результат, который будет меньше делителя, должен быть увеличен за счет следующей цифры в ряду делимого. Далее ученик записывает 4 к уже вычисленной четверке.

5 Этап. Дальнейшее объяснение действий лежит в уже знакомой ребенку плоскости математической логики и требует ответа на вопрос о том, — сколько раз число 8 помещается в числе 44? Вспомнив навыки таблицы умножения «наизнанку», ребенок должен дать ответ — это 8. Взрослый поясняет школьнику, что это теперь будет следующая цифра в записи результата частного, которое он продолжает вычислять. Далее следует умножение им 5 на 8 и полученный результат, 40, следует записать под цифрой 44 в столбике.

6 Этап. Здесь операция повторяется и действия обучаемого идут по «накатанному пути». Ребенок вычтет 40 из числа 44, получив 4

Ещё раз взрослому стоит заострить его внимание на том, что 4 меньше делителя 5 и значит действия ребенок выполняет правильно. Предстоит использовать последнюю цифру, оставшуюся у делимого – 5

Дописав ее вниз по столбику к четверке ребенок получит число 45.

Взрослый повторяет вопрос в отношении этого результата. Сколько пятерок в числе 45? Ответом станет число 9, которое и надо записать под чертой.

7 Этап. Завершающий, на нем надо попросить ученика умножить 5 на 9. Школьник должен получить результат 45, озвучив его он делает запись в столбике под цифрой 45. Проделав операцию вычитания 45 из 45 ученик получит 0. При получении этого результата взрослый поясняет школьнику, что им был только что рассмотрен пример деления числа без остатка столбиком.

Как уже всем стало наверно понятно, — ключом к быстрому и эффективному умению делить столбиков для ребенка является его умение пользоваться таблицей умножения. Дальнейшие навыки закрепляются систематическим выполнением примеров и упражнений ребенком сначала под контролем взрослого, а затем уже самостоятельно.

Основные понятия

Во всем мире принято использовать эти десять цифр для записи чисел: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. С их помощью создается любое натуральное число.

Название числа напрямую зависит от количества знаков.

• Однозначное — состоит из одного знака
• Двузначное — из двух
• Трехзначное — из трех и так далее.

Разряд — это позиция, на которой стоит цифра в записи. Их принято отсчитываются с конца.

Разряд единиц — то, чем заканчивается любое число. Разряд десятков — то, что находится перед разрядом единиц. Разряд сотен стоит перед разрядом десятков. На место отсутствующего разряда всегда можно поставить ноль.

В числе 429 содержится 0 тысяч, 4 сотни, 2 десятка и 9 единиц.

Умножение — арифметическое действие в котором участвуют два аргумента. Один множимый, второй множитель. Результат их умножения называется произведением.

Свойства умножения 1. От перестановки множителей местами произведение не меняется. a * b = b * a 2. Результат произведения трёх и более множителей не изменится, если любую группу заменить произведением. a * b * c = (a * b) * c = a * (b * c) Самое главное в процессе вычисления — это знание таблицы умножения. Это сделает подсчет упорядоченным и быстрым.

Важно помнить правило: умножение в столбик с нулями дает в результате ноль

а * 0 = 0, где а — любое натуральное число.

Алгоритм умножения в столбик

Чтобы понять, как умножать в столбик — рассмотрим действия по шагам:

1. Запишем пример в строку. Выберем и подчеркнем из двух чисел наименьшее, чтобы не забыть при новой записи поставить его вниз.

2. Записываем произведение в виде столбика. Сначала наибольший множитель, затем наименьший, тот что мы подчеркнули ранее. Слева ставим соответствующий знак и проводим черту под которой будем записывать ход решения

Важно обратить внимание разряды, чтобы единицы стояли стоять под единицами, десятки под десятками и т. д

3. Поэтапно производим необходимые действия. Каждую цифру первого множителя нужно умножить на крайнюю цифру второго. Это действие происходит справа налево: единицы, десятки, сотни.

Если результат получится двузначным, под чертой записывается только последняя его цифра. Остальное переносим в следующий разряд путем сложения со значением, полученным при следующем умножении.

4. После умножения на единицу второго множителя с остальными цифрами необходимо провести аналогичные манипуляции. Результаты записывать под чертой, сдвигаясь влево на одну позицию.

5. Складываем то, что нашли и получаем ответ.

Умножение на однозначное число

Для решения задачи по произведению двух натуральных чисел, одно из которых однозначное, а другое — многозначное, нужно использовать способ столбика. Для вычисления воспользуемся последовательностью шагов, которую рассмотрели выше. 

Возьмем пример 234 * 2:

1. Запишем первый множитель, а под ним второй. Соответствующие разряды расположены друг под другом. Двойка находится под четверкой.

2. Последовательно умножаем каждое число в первом множителе на второй, начиная с единиц и продвигаясь к десяткам и сотням.

3. Ответ запишем под чертой:

Производить действия необходимо в следующей последовательности:

Умножение двух многозначных чисел

Если оба множителя — многозначные натуральные числа, нужно действовать следующим образом.

Рассмотрим пример 207 * 8063:

1. Сначала запишем наибольшее 8063, затем наименьшее 207. Нужно разместить цифры друг под другом справа налево:

1. Последовательно перемножаем значения разрядов. Результатом является неполное произведение.

1. Далее перемножаем десятки. Первый множитель умножим на значение разряда десятков второго и т.д. Результат запишем под чертой.

1. По аналогии действуем с сотыми. Ноль пропускаем в соответствии с правилом. Так получилось второе неполное произведение:

1. Далее складываем два произведения в столбик. 

1. Получившееся семизначное число — результат умножения исходных натуральных чисел.

Ответ: 8 063 * 207 = 1669041. 

Примеры на умножение в столбик

Самостоятельное решение задачек помогает быстрее запомнить правила и натренировать скорость

Неважно, в каком классе учится ребенок — в 1, 3 или 4 — эти примеры подойдут всем

Повтори тему — деление в столбик, она очень полезная!

Деление в столбик на двузначное число

Деление в столбик школьники проходят еще в младших классах на уроках математики. В дальнейшем его применяют как вспомогательное средство при решении задач. Но если не пройти в нормальном виде деление уголков, то могут возникнуть затруднения и с трехзначными числами.

Рис. 1

На рисунке 1 показан принцип деления и названия основных элементов процесса. Как и при делении на однозначные числа, работает алгоритм перехода от крупных к мелким единицам.

Порядок действий опишем, взяв для примера вычисление, представленное на рисунке 1:

1. Выделить самое маленькое двузначное число 63, которое можно поделить на делитель 61. Оно всегда больше того, которое является делителем.

2. Делим 63 на 61. Сколько раз 61 поместится в 63? Один. Записываем под уголком единицу. Это первая цифра частного.

3. Умножаем делитель на эту первую цифру: 61 * 1 = 61, вычитаем из 63 число 61, проводим черту и пишем разность — 2.

4. Сносим следующую цифру делимого — 4. Получаем число 24. Оно не делится на 61, потому записываем ноль на место второй цифры частного (это место рядом с цифрой 1 в нашем примере).

5. Сносим следующую (последнюю в нашем примере) цифру, это 4. Получаем число 244. Делим его на 61. Применим правило устного деления, описанное выше. Нужно подобрать такую цифру, которая при умножении на последнюю цифру (у 61 последняя цифра 1) даст ответ, оканчивающийся на последнюю цифру делимого (у 244 последняя цифра 4, она нам и нужна). Т. е. 4 * 1 = 4. Проверка: 61 * 4 = 244. Мы подобрали цифру 4 и она нам подошла.

6. Вписываем 4 третьей цифрой частного в уголок, получаем 104. Умножаем 61 на 4 и вычитаем результат из 244. Получаем 0. Деление выполнено.

В данном примере делимое — трёхзначное число. В общем случае процесс сноса цифр делимого и деления их на делитель продолжается до тех пор, пока не закончатся все цифры делимого. Этот принцип подходит для трехзначных, четырехзначных и других многозначных чисел.