Деление многочлена на многочлен «уголком»

Как научиться делить столбиком трехзначные числа

Когда в делителе стоит трехзначное число, действие лучше всего выполнять в столбик. Алгоритм математического решения аналогичен делению на двузначное число.

Для примера рассмотрим следующие действия: 146676 : 719

146<719, поэтому сразу возьмем четырехзначное число «1466». В данном значении помещается 2 делителя: 719 х 2= 1438. Цифра «2» будет первым значением частного. Ее запишем справа под уголком.

1466 — 1438 = 28. Полученную разность запишем под чертой слева. Снесем к 28 цифру «7». 287<719, поэтому рядом с двойкой запишем «0».

Снесем последнюю цифру делимого «6», в итоге получится число «2876», которое разделим на 719. Возьмем по 3: 719 х 3 = 2157 — мало, можно взять по 4: 719 х 4 = 2876. Цифру «4» запишем рядом с «20», получим в ответе 204. От 2876 отнимем 2876 , получим разность 0.

Обучение делению с остатком

Когда ребенок усвоит материал о делении, можно усложнять задачу. Деление с остатком – это следующая ступень обучения. Объяснять нужно на доступных примерах:

• Предложите ребенку разделить 35 на 8. Запишите в столбик задачу.
• Чтобы ребенку было максимально понятно, можно показать ему таблицу умножения. В таблице наглядно видно, что в число 35 входит 4 раза число 8.
• Запишите под числом 35 число 32.
• Ребенку нужно от 35 вычесть 32. Получится 3. Число 3 является остатком.

Деление с остатком

Простые примеры для ребенка

На этом же примере можно продолжить:

• При делении 35 на 8 получается остаток 3. К остатку нужно дописать 0. При этом после цифры 4 в столбике нужно поставить запятую. Теперь результат будет дробным.
• При делении 30 на 8 получается 3. Эту цифру нужно записать после запятой.
• Теперь нужно под значением 30 написать 24 (результат умножения 8 на 3). В итоге получится 6. К цифре 6 тоже нужно дописать ноль. Получится 60.
• В число 60 помещается цифра 8 входит 7 раз. То есть, получится 56.
• При вычитании 60 от 56 получается 4. К этой цифре тоже нужно подписать 0. Получается 40. В таблице умножения ребенок может увидеть, что 40 – это результат умножения 8 на 5. То есть, в число 40 цифра 8 входит 5 раз. Остатка нет. Ответ выглядит так – 4,375.

Данный пример может показаться ребенку сложным. Поэтому нужно много раз делить значения, у которых будет остаток.

Как правильно делить числа в столбик: алгоритм деления

алгоритм деления чисел столбиком

Для деления чисел столбиком следуйте по таким шагам:

• правильно запишите действие деления на бумаге. Выбирайте верхний правый угол тетради/листа. Если вы только учитесь выполнять действие деления в столбик, берите бумагу в клетку. Так вы сохраните визуальную последовательность решения,
• разлинейте место между делимым и делителем.
  Вам поможет схема ниже.

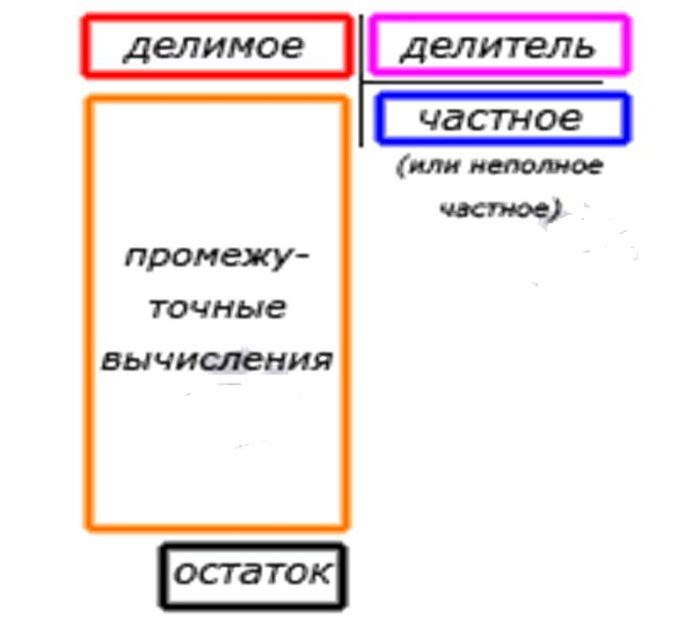
схема и назнвания составных элементв действия деления чисел столбиком

• планируйте пространство для деления в столбик. Чем длиннее число, которое подлежит делению, и чем корове делитель, тем ниже на станице спуститься решение,
• первое действие деления совершайте с тем количеством цифр делимого, которое равно делителю. Например, если справа от разделительной линии у вас стоит однозначная цифра, то рассматривайте первую у делимого, если двухзначная — то 2 первых,
• перемножьте числа под и над чертой и запишите результат под цифрами делимого, которые вы обозначили для первого действия,
• завершайте действие вычитанием и определением остатка. Нарисуйте горизонтальную линию над ним, чтобы отделить первый шаг решения,
• допишите следующую цифру делимого к остатку и продолжайте решение,
• последний шаг деления — когда вы получите от вычитания 0 либо число, меньше делителя. Во втором случае ваш ответ будет с остатком, например, 17 и 3 в остатке.

Обучение делению в столбик в тетради

Начинать обучение нужно тогда, когда ученик понял материал о делении на практике, с помощью игры и таблицы умножения.

Пример деления

Нужно начинать делить таким образом, применяя простые примеры. Так, деление 105 на 5.

Объяснять математическое действие нужно подробно:

• Напишите в тетради пример: 105 разделить на 5.
• Запишите это, как при делении в столбик.
• Расскажите, что 105 – делимое, а 5 – делитель.
• С учеником определите 1 цифру, которая допускает деление. Значение делимого – 1, эта цифра не делится на 5. А вот второе число – 0. В итоге получится 10, это значение допускается разделить данный пример. Число 5 два раза входит в число 10.
• В столбике деления, под числом 5, напишите цифру 2.
• Попросите ребенка число 5 умножить на 2. По итогу умножения получится 10. Это значение нужно записать под числом 10. Далее нужно написать в столбике знак вычитания. От 10 нужно отнять 10. Получится 0.
• Запишите в столбике число, получившееся в результате вычитания – 0. У 105 осталось число, которое не участвовало в делении – 5. Это число нужно записать.
• В итоге получится 5. Это значение нужно разделить на 5. Результат – цифра 1. Это число нужно записать под 5. Результат деления – 21.

Родителям нужно объяснить, что это деление не имеет остатка.

Начать деление можно с цифр 6,8,9, затем переходить к 22, 44, 66, а после к 232, 342, 345, и так далее.

Еще один пример деления

Правило встречается в следующих упражнениях:

3 класс

Страница 76,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 59. Вариант 2. Тест 1,
Моро, Волкова, Проверочные работы

Страница 28,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 32,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 34,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 99,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 34,
Моро, Волкова, Рабочая тетрадь, часть 2

Страница 40,
Моро, Волкова, Рабочая тетрадь, часть 2

Страница 44,
Моро, Волкова, Рабочая тетрадь, часть 2

Страница 58,
Моро, Волкова, Рабочая тетрадь, часть 2

4 класс

Страница 35,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 54,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 79,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 62. Вариант 1. Проверочная работа 2,
Моро, Волкова, Проверочные работы

Страница 5,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 18,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 26,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 63,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 76,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 55,
Моро, Волкова, Рабочая тетрадь, часть 2

5 класс

Задание 533,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 545,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 550,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 599,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 954,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1082,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1091,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1161,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1167,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Номер 767,
Мерзляк, Полонский, Якир, Учебник

6 класс

Номер 179,
Мерзляк, Полонский, Якир, Учебник

Номер 3,
Мерзляк, Полонский, Якир, Учебник

Номер 373,
Мерзляк, Полонский, Якир, Учебник

Номер 499,
Мерзляк, Полонский, Якир, Учебник

Номер 1098,
Мерзляк, Полонский, Якир, Учебник

Номер 1149,
Мерзляк, Полонский, Якир, Учебник

Задание 477,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 601,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1083,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1134,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

7 класс

Номер 32,
Мерзляк, Полонский, Якир, Учебник

Номер 47,
Мерзляк, Полонский, Якир, Учебник

Деление на двузначное число

Когда ученик 3-го класса усвоил деление на однозначное число, можно приступать к следующему этапу — работе с двузначными цифрами. Начинайте с простых, явных примеров, чтобы малыш понял алгоритм действий при делении на двузначные числа. Например, возьмите числа 196 и 28 и объясните принцип:

1. Сначала подберите примерное число для ответа. Для этого выясните приблизительно, сколько цифр 28 поместится в 196. Для удобства можно округлять оба числа: 200:30. Получится не больше 6. Полученное число не нужно записывать, это только догадка.

2. Проверяем результат умножением: 28х6. Получается 196. Предположения оказались верными.

3. Запишите ответ: 196:28 =6.

Еще один вариант обучения: деление на двузначное число уголком. Такой способ больше подходит для работы с числами от четырех разрядов, то есть тысяч. Приведем простой пример:

Напишите на листе бумаги 4070, начертите уголок и подпишите делитель — 74.
Определите, с какого числа начнете делить. Спросите у ребенка, можно ли разделить 4 на 74, 40? В результате малыш поймет, что сначала нужно ограничиться числом 407. Очертите полученную цифру сверху полукругом. 0 останется в стороне.
Теперь нужно выяснить, сколько 74 поместится в 407. Действуем с помощью логики и проверки умножением. Получится 5. Записываем результат под уголком (под делителем).
Теперь умножаем 74 на 5 и записываем результат под делимым. Получится 370

Важно начинать запись с первого числа слева.
После записи нужно подвести горизонтальную черту и отнять 370 от 407. Получится 37.
37 разделить на 74 нельзя, поэтому вниз сносится оставшийся в верхнем ряду 0.
Теперь делим 370 на 74

Подбираем множитель (5) и записываем его под уголком.
Умножаем 5 на 74, записываем результат в столбик. Получится 370.
Опять получаем разность. Результат будет равен 0. Значит, деление считается завершенным без остатка.

4070:74=55. Частное смотрим под уголком.

Для проверки правильности решение произведите умножение: 74х55=4070.

Деление на двузначное число с остатком

Действует ли при делении с остатком какой-либо другой алгоритм? Нет! При делении с остатком рассуждают точно так же, как и при делении без остатка.

Ребята, какое правило нужно знать и обязательно проверять при делении с остатком?

А теперь решите самостоятельно примеры на деление с остатком. Не забывайте сравнивать остаток с делителем, сделайте проверку.

272 : 98    495 : 46    385 : 65   321 : 47

Проверь себя.

Ребята, в каком примере вы встретили затруднение? Рассмотрим вместе пример

495 : 46

Почему в частном появился 0 (нуль)?

Первое неполное делимое 49. Делим на 46. Берем по 1. Остаток 3 меньше делителя 46. Делим верно. Сносим следующую цифру 5.

35 делим на  46. Берем по 0 (35 меньше, чем 46).  Остаток 35 меньше делителя, разделили верно. Сделаем проверку, убедимся в правильности вычислений.

Уметь делить с остатком – полезный навык, который не раз поможет вам в решении практических задач. Например, для постройки одинаковых башен у вас имеется 430 деталей лего-конструктора. Сколько башен можно построить, если на каждую нужно 35 деталей? Останутся ли лишние детали?

Давайте вместе решим эту задачу.

430 разделим на 35. Сделаем это столбиком (уголком).

Мы видим, что при делении получился остаток 10. Делаем вывод: из 430 деталей лего-конструктора можно сделать 12 одинаковых башен и еще 10 деталей останется.

Разделить можно на черновике, а решение в тетради записать в строчку.

430 : 35 = 12 (ост.10) – башен можно сделать.

Ответ: 12 башен и 10 деталей останется.

Если вы хорошо умеете делить с остатком, решение можно сразу записать в тетрадь:

Решите самостоятельно практическую задачу.

Задача

Ребята 4 класса изготовили для первоклассников 126 закладок в учебники. Сколько закладок достанется каждому первокласснику, если в первом классе 25 учеников? Останутся ли лишние закладки?

Проверь себя.

Деление в столбик двузначных, трехзначных, многозначных чисел, чисел с нулями

Не нужно пугаться сразу, что процесс деления не простой, поэтому вы не освоите его. Освоите! В математике следует соблюдать четкие правила, тогда у вас все получится. Алгоритм деления лучше учить на конкретных примерах, ниже будет представлено множество примеров.

Пример деления на трехзначный делитель

Все они выполняются по схеме:

1. Вначале записывается делимое, рядом ставится значок разделить: Ι—, и над чертой пишется делитель (число, на которое делят делимое).
2. Потом необходимо выделить часть делимого для осуществления деления, если это необходимо в данном случае.
3. Далее придется выполнять умножение для того, чтобы определить, сколько раз взять делитель, чтобы получилась выделенная часть делимого. Причем число не должно быть больше 9-ти.
4. Выполняете умножение делителя, записываете результат под делимым, а число ≤ 9-ти записываете под черту знака: Ι– разделить.
5. Из выбранной части делимого вычитаете результат, записываете его под подчеркиванием, сносите следующую цифру делимого, повторяйте опять процесс умножения, пока не разделите число на число.

Рассмотрим деление в столбик на простом примере:

Если такие двухзначные числа, как 16, 28 можно разделить в уме на 2 или 4 (в первом случае при делении на 2 получится 8 и 14), а во втором (4 и 7), то 51 разделить на 3 без столбика уже сложнее. Как происходит деление в столбик распишем на примере 51 разделить на 3.

Деление в столбик

• Как записывается делимое, делитель уже было сказано, визуально можно посмотреть выше на изображении. Делимое идет первым, потом ставится значок деления и над чертой пишут делитель.
• Теперь определяемся, сколько выделить цифр, чтобы начать подбирать множитель, который записывается под чертой в выделенный квадратик на изображении.
• Выделяем одну цифру 5-ку, она больше 3-ки, на черновике распишите примерно какой подобрать множитель, для того чтобы получить число ≤ 5, наглядно это выглядит так: 5 ≥ 3 · 1, число 1 и есть множитель. Его пишут под чертой делить в квадратике.
• Далее под пятеркой пишем произведение 3 · 1 = 3.
• Теперь вычитаем из 5 — 3 = 2. Разница, в нашем случае 2 должна быть < делителя, в нашем случае 3.
• Итак, остается разделить 21 на 3. Из таблицы умножения вы знаете, что: 21 : 3 = 7.
• Семерку пишут под чертой значка делить после единицы. Ответ получается 17.

Далее рассмотрим пример деления трехзначных чисел:

Давайте разделим трехзначное число 512 на 16. Деление будет происходить по той же схеме, что и двухзначного числа.

Пример деления трехзначного числа

• Запишите делимое, делитель, как на фото выше.
• Далее выделим число 51, и узнайте, сколько раз нужно взять число 16, чтобы получилось произведение меньше или равно 51. Итак, выше представлены расчеты: 16 · 3 = 48 < 51.
• Значит под чертой напишите 3, а под делимым 48. Теперь из 51 вычтите 48, получится 3, сносим следующую цифру 2.
• Подберите множитель к 16, чтобы произведение получилось равное или меньше 32. Итого: 16 · 2 = 32.
• Двойку запишите под черту знака деления, а результат 32 под делимым. Итого 32 — 32 = 0.
• Результат 32.

Рассмотрим деление многозначного числа:

Давайте найдем частное 998190 на 135, пример представлен на изображении ниже. Чтобы решить его, следует подставить нужные числа в пустых клетках.

Пример деления в столбик

• Итак, нужно найти первую цифру, на которое нужно умножить число 135, чтобы получить результат ≤ 998. Для этого понадобится знать отлично таблицу умножения и умение складывать цифры. 135 · 7 = 945.
• Число 945 пишите под делимым, вычтите из 998 — 945 = 53. Это число меньше 135, потому нужно снести еще одну цифру 1, получится 531.
• Высчитываем, какой множитель подойдет, к 135, чтобы получить число меньше, чем 534. Решение: 135 · 3 = 405.
• Вторая цифра под чертой знака деления 3, из 531 — 405 = 126.
• Сносим 9, выходит 1269, подбираем множитель к 135. Результат 135 · 9 = 1215.
• Третья цифра под чертой 9. Теперь: 1269 — 1215 = 54.
• Сносим 0, выходит 540, а 540 = 135 · 4, итого последняя цифра результата это 4.
• Результат 7394.

Деление чисел с нулями:

Умножение многочленов столбиком

Также можно умножать многочлены столбиком, аналогично умножению целых чисел. Рассмотрим конкретные примеры.

Пример умножения многочленов столбиком

Найти произведение многочленов: .

Решение

Умножаем многочлены столбиком.

1   Записываем исходные многочлены друг под другом в столбик и проводим черту.

2.1   Умножаем младший член второго многочлена на первый многочлен: . Результат записываем в столбик.

2.2   Умножаем следующий член второго многочлена на первый многочлен: . Результат записываем в столбик, выравнивая степени .

2.3   Умножаем следующий (старший) член второго многочлена на первый многочлен: . Результат записываем в столбик, выравнивая степени .

3   После того, как все члены второго многочлена умножили на первый, проводим черту и складываем члены с одинаковыми степенями ; ; ; .

Заметим, что можно было записывать только коэффициенты, а степени переменной можно было опустить. Тогда умножение столбиком многочленов будет выглядеть так:

Ответ

.

Пример 2

Найти произведение многочленов столбиком: .

Решение

При умножении многочленов столбиком важно записывать одинаковые степени переменной друг под другом. Если некоторые степени пропущены, то их следует записывать явно, умножив на нуль, либо оставлять пробелы

В этом примере некоторые степени пропущены. Поэтому запишем их явно, умноженными на нуль: . Умножаем многочлены столбиком.

1   Записываем исходные многочлены друг под другом в столбик и проводим черту.

2.1   Умножаем младший член второго многочлена на первый многочлен: . Результат записываем в столбик.

2.2   Следующий член второго многочлена равен нулю. Поэтому его произведение на первый многочлен также равно нулю. Нулевую строку можно не записывать.

2.3   Умножаем следующий член второго многочлена на первый многочлен: . Результат записываем в столбик, выравнивая степени .

2.3   Умножаем следующий (старший) член второго многочлена на первый многочлен: . Результат записываем в столбик, выравнивая степени .

3   После того, как все члены второго многочлена умножили на первый, проводим черту и складываем члены с одинаковыми степенями .

Ответ

.

Правила записи при делении столбиком

Начнем с изучения правил записи делимого, делителя, всех промежуточных выкладок и результатов при делении натуральных чисел столбиком. Сразу скажем, что письменно выполнять деление столбиком удобнее всего на бумаге с клетчатой разлиновкой – так меньше шансов сбиться с нужной строки и столбца.

Сначала в одной строке слева направо записываются делимое и делитель, после чего между записанными числами изображается символ вида . Например, если делимым является число 6 105, а делителем – 55, то их правильная запись при делении в столбик будет такой:

Посмотрите на следующую схему, иллюстрирующую места для записи делимого, делителя, частного, остатка и промежуточных вычислений при делении столбиком.

Из приведенной схемы видно, что искомое частное (или неполное частное при делении с остатком) будет записано ниже делителя под горизонтальной чертой. А промежуточные вычисления будут вестись ниже делимого, и нужно заранее позаботиться о наличии места на странице. При этом следует руководствоваться правилом: чем больше разница в количестве знаков в записях делимого и делителя, тем больше потребуется места. Например, при делении столбиком натурального числа 614 808 на 51 234 (614 808 – шестизначное число, 51 234 – пятизначное число, разница в количестве знаков в записях равна 6−5=1) для промежуточных вычислений потребуется меньше места, чем при делении чисел 8 058 и 4 (здесь разница в количестве знаков равна 4−1=3). Для подтверждения своих слов приводим законченные записи деления столбиком этих натуральных чисел:

Теперь можно переходить непосредственно к процессу деления натуральных чисел столбиком.

Как научиться делить столбиком

Деление столбиком с остатком и без него нельзя начинать без подготовки. Сначала ребенок должен хорошо уметь и знать следующее:

• Разряды натуральных чисел (десятки, сотни, тысячи). Находить их в ряду многозначных цифр.
• Таблица умножения. Этот материал лучше выучить наизусть и постоянно повторять.
• Отнимать, складывать не только однозначные или двузначные, но и многозначные числа.
• Решать маленькие задачи на умножение, разность, сумму устно.

Отработайте все обозначенные умения до автоматизма. Затем приступайте к делению маленьких цифр на примере таблицы умножения в уме. Например, ребенок выучил, как умножать цифру 6:

6х2=12

6х3=18

6х4=24 и так далее.

Смело предлагайте такие примеры:

24:6=4

24:4=6

12:2=6

18:3=6

Через пару уроков школьник будет выполнять такие задания легко. Можно разнообразить занятия по устному счету играми на деление.

Игровые задания

Интересные математические игры на деление без остатка помогают детям закрепить навык, узнать законы работы с цифрами, освоить устный счет.

• Головоломки на развитие внимания. Напишите в тетради 3–5 примеров на деление с ответами.

  Все, кроме одного, должны быть решены неверно. Нужно быстро найти тот пример, который содержит правильный ответ. Затем исправить остальные примеры с помощью устного счета.

• Подбор примера по результату. Предлагайте малышу ответ без примера. Давайте задание придумать задачу. Например, ответ 8. Ребенок может придумать такую задачу: 48:6.
• «Идем в магазин». Расставьте на полу игрушки с карточками. На листах написаны примеры: 6:2, 18:3, 42:7, 100:50. Игрушки — это «товар» в фантазийном магазине, частное после решения примера на карточке — их цена. Чтобы узнать стоимость покупки, нужно решить задания, а потом оплатить полученный результат в кассу. Играть лучше в небольшой команде — 2–3 человека.
• «Молчуны». Ребенок получает карточки с цифрами от 1 до 100. Задавайте вопросы с примерами на деление, ученик должен отвечать без слов, показывая правильный ответ.
• Небольшие самостоятельные работы с подарком за старательность. Распечатайте карточки с примерами в количестве 5–10 штук. Укажите время на решение, например 5 минут. Поставьте перед ребенком песочные часы. После выполнения контрольной верно поощрите школьника походом в зоопарк, кино, покупкой книги, сладостей. Такой тренажёр хорошо стимулирует детей.

• «Ищем дерево».

  Нарисуйте небольшой сад с деревьями на картоне. Каждому растению дайте номер, пусть их будет 10. На листочке для ученика напишите 3 примера:

45:9           120:60          14:7

Школьник должен вычислять результат к каждому заданию, а потом складывать все числа между собой. Получится так:

45:9=5

120:60=2

14:7=2

5+2+2=9

Ребенок должен найти дерево под номером 9.

Для игры можно использовать цветные пуговицы и ставить их на занятые деревья. Развлечение подходит для командных соревнований.

После устной работы с делением натуральных чисел можно показать ребенку порядок записи примеров столбиком. Если педагогического опыта у вас нет и вы не знаете, как объяснить ребёнку процесс деления столбиком, то посмотрите видеоурок на эту тему, вспомните теорию сами.

Теперь можно приступать к объяснению сложного материала школьнику. Есть несколько методик домашнего обучения делению:

1. Мама-учитель

Родителям придется ненадолго стать педагогами. Оборудовать доску, купить мел или маркеры. Заранее вспомнить школьный материал по теме “деление уголком”. Объяснить пошагово теорию и закрепить ее на практике с помощью большого количества самостоятельных, карточек, контрольных работ.

Например, это:

Затем нужно обсуждать с малышом материал, закреплять навык на практике несколько недель.

3. Нанять репетитора

Деление (даже трёхзначных чисел на двузначные) не самая сложная тема в школьной программе. В начальных классах можно легко обойтись без платных уроков с педагогом.

Этот вариант оставим на крайний случай.

Проверка деления с остатком

Пока решаешь пример, бывает всякое: то в окно отвлекся, то друг позвонил

Чтобы убедиться в том, что все правильно, важно себя проверять. Особенно ученикам 5 класса, которые только начали проходить эту тему

Формула деления с остатком a = b * c + d, где a — делимое, b — делитель, c — неполное частное, d — остаток.

Эту формулу можно использовать для проверки деления с остатком.

Пример

Рассмотрим выражение: 15 : 2 = 7 (остаток 1).

В этом выражении: 15 — это делимое, 2 — делитель, 7 — неполное частное, а 1 — остаток.

Чтобы убедиться в правильности ответа, нужно неполное частное умножить на делитель (или наоборот) и к полученному произведению прибавить остаток. Если в результате получится число, которое равно делимому, то деление с остатком выполнено верно. Вот так:

• 7 * 2 + 1 = 15;
• 2 * 7 + 1 = 15.

Как делить столбиком числа с нулями?

улыбчивая девочка у школьной доски

Последовательность и алгоритм действий аналогичен классическому, рассмотренному в первом разделе.

Из нюансов отметим:

• при наличии нулей в конце делителя и делимого смело сокращайте их. Предложите ребёнку зачеркнуть их карандашом и продолжить деление как обычно. Например, в ситуации 1200:400 ребёнок может убрать оба нуля у обоих чисел, но в ситуации 15600:560 — только по одному крайнему,
• если ноль есть только в делителе, то подбирайте первую цифру для действия, ориентируясь на число перед ним. Например, в примере 6537:70 поставьте 9 в частное первым числом. Для данного примера совершайте умножение на обе цифры делителя и подписывайте их под тремя у делимого.

Когда нулей у делимого много и процесс деления закончился до того, как вы их все использовали, то перенесите их в частное после цифр, которые образовались до этого. Пример, 1000:2=500 — вы перенесли два последних нуля.

Итак, мы рассмотрели основные ситуации деления чисел разного количества разрядности в столбик, определили алгоритм действия и акценты для обучения ребёнка.

Практикуйте полученные знания и помогайте своему чаду осваивать математику.

Письменное деление на трехзначное число

Ребята, как вы думаете, отличается ли алгоритм деления на трехзначное число от знакомого нам алгоритма на двузначное число?

Нет, не отличается! Давайте повторим последовательность наших действий при делении столбиком.

Используя данный алгоритм, решим вместе несколько примеров. Будем делать записи в черновике. Вы знаете, что цифры в частном – пробные, и требуется  проверка.

984 : 123        1 155 : 9        318 : 106        5 850 : 9

Оставшиеся примеры на деление решите самостоятельно. Проверьте себя по образцу.

Проверь себя.

При делении многозначных чисел столбиком ребята часто пропускают нули в частном. Обидная ошибка! Как этого не допустить? Рассмотрим более сложные случаи деления, когда в частном появляются нули.

Есть маленькие секреты безошибочного деления столбиком!

• Обязательно определяйте количество цифр в частном. Даже если вы случайно пропустили нуль, точки подскажут, что цифр в частном недостаточно.
• Делайте проверку: умножьте делитель на частное. Должно получиться делимое.

А теперь решите самостоятельно  пример. Подумайте, нужен ли нуль в частном. Сравните свое решение с образцом.

55 692 : 273

Проверь себя.

Как научить ребенка делению – закрепляем навык

Главное из-за чего у многих школьников возникает проблема с математикой — это неумение быстро делать простые арифметические расчеты. А на этой основе построена вся математика в начальной школе. Особенно часто проблема именно в умножении и делении.
Чтобы ребенок научился быстро и качественно проводить расчеты деления в уме — необходима правильная методика обучения и закрепление навыка. Для этого мы советуем воспользоваться популярными на сегодня пособиями в усвоение навыка деления. Одни предназначены для занятий детей с родителями, другие для самостоятельной работы.

1. «Деление. Уровень 3. Рабочая тетрадь» от крупнейшего международного центра дополнительного образования Kumon
2. «Деление. Уровень 4. Рабочая тетрадь» от Kumon
3. «Не Ментальная арифметика. Система обучения ребенка быстрому умножению и делению. За 21 день. Блокнот-тренажёр.» от Ш. Ахмадулина – автора обучающих книг-бестселлеров

Самым главным, когда вы учите ребёнка делению в столбик, является  усвоение алгоритма, который, в общем-то, достаточно прост.

Если ребёнок хорошо оперирует таблицей умножения и «обратным» делением, у него не возникнет трудностей

Тем не менее очень важно постоянно тренировать полученный навык. Не останавливайтесь на достигнутом, как только вы поймёте, что ребёнок уловил суть метода

Для того чтобы легко научить ребёнка операции деления нужно:

• Чтобы в возрасте двух–трех лет он освоил отношения «целое – часть». У него должно сложиться понимание целого, как неразделимой категории и восприятие отдельной части целого как самостоятельного объекта. Например – игрушечный грузовик – целое, а его кузов, колеса, дверцы – части этого целого.
• Чтобы в младшем школьном возрасте ребенок свободно оперировал действиями по сложению и вычитанию чисел, понимал суть процессов умножения и деления.

Для того чтобы занятия математикой доставляли ребёнку удовольствие, необходимо возбуждать его интерес к математике и математическим действиям, не только во время обучения, но и в бытовых ситуациях.

Поэтому поощряйте и развивайте наблюдательность у ребёнка, проводите аналогии с математическими действиями (операции на счёт и деление, анализ отношений «часть-целое» и т.д.) во время конструирования, игр и наблюдений за природой.