Математика 4 класс

Признак делимости на 4, примеры

Мы можем пойти простым путем и поделить однозначное натуральное число на 4 для того, чтобы проверить, делится ли это число на 4 без остатка. Так же можно поступить с двузначными, трехзначными и проч. числами.  Однако, чем больше становятся числа, тем сложнее проводить с ними действия с целью проверки делимости их на 4.

Гораздо проще становится использовать признак делимости на 4. Он предполагает проведение проверки делимости одной или двух последних цифр целого числа на 4. Что это значит? Это значит, что некоторое число a делится на 4 в том случае, если одна или две крайние правые цифры в записи числа a делятся на 4. Если число, составленное из двух крайних правых цифр в записи числа a не делятся на 4 без остатка, то и число a не делится на 4 без остатка.

Пример 1

Какие из чисел 98 028, 7 612 и 999 888 777 делятся на 4?

Решение

Крайние правые цифры чисел − 98 028, 7 612 составляют числа 28 и 12, которые делятся на 4 без остатка. Это значит, что и целые числа − 98 028, 7 612​​​​​​ ​делятся на 4 без остатка.

Последние две цифры в записи числа 999 888 777 образуют число 77, которое не делится на 4 без остатка. Это значит, что и исходное число на 4 без остатка не делится.

Ответ: −98 028 и 7 612.

Если предпоследней цифрой в записи числа является , то нам необходимо этот ноль отбросить и смотреть на оставшуюся крайнюю правую цифру в записи. Получается, что две цифры 01 мы заменяем 1. И уже по одной оставшейся цифре мы делаем вывод о том, делится ли исходное число на 4.

Пример 2

Делится ли числа 75 003 и −88 108 на 4?

Решение

Две последние цифры числа 75 003 — видим 03. Если отбросить ноль, то у нас остается цифра 3, которая на 4 без остатка не делится. Это значит, что исходное число 75 003 на 4 без остатка не делится.

Теперь возьмем две последние цифры числа −88 108. Это 08, из которых мы должны оставить лишь последнюю цифру 8. 8 делится на 4 без остатка.

Это значит, что и исходное число −88 108 мы можем поделить на 4 без остатка.

Ответ: 75 003 не делится на 4, а −88 108 – делится.

Числа, у которых в конце записи идет сразу два нуля, также делятся на 4 без остатка. Например, 100 делится на 4, получается 25. Доказать правдивость этого утверждения нам позволяет правило умножения числа на 100.

Представим произвольно выбранное многозначное число a, запись которого справа заканчивается двумя нулями, как произведение a1·100, где число a1 получается из числа a, если в его записи справа отбросить два нуля. Например, 486700=4867·100.

Произведение a1·100 содержит множитель 100, который делится на 4. Это значит, что все приведенное произведение делится на 4.

Задачи на нахождение площади

1. Найдите площадь и периметр прямоугольника со сторонами 8 см и 9 см. 679. Длина прямоугольника 7 дм, ширина 3 дм. Чему равны площадь и периметр прямоугольника?2. Площадь фундамента дома квадратной формы 64 кв. м. Чему равен периметр дома?3. Длина прямоугольника 6 дм, ширина 4 см. Чему равны площадь и периметр прямоугольника?4. Длина прямоугольника 4 м, ширина 3 дм. Чему равны площадь и периметр прямоугольника? 5. Ширина вагона 3 м, а длина 750 см. Чему равны площадь и периметр вагона?6. Высота зеркала 180 см, ширина 70 см. Чему равны площадь и периметр зеркала?7. Длина прямоугольника равна стороне квадрата с периметром 48 см, а ширина его в 4 раза меньше. Чему равны площади прямоугольника и квадрата?8. Чему равны площади всех возможных прямоугольников с периметром 18 см, если длина их сторон выражена целым числом сантиметров. У какого прямоугольника площадь наибольшая?9. Детская площадка была длиной 16 м и шириной 14 м. После переделки её увеличили в длину на 4 м и уменьшили в ширину на 3 м. Как изменилась площадь детской площадки?10. Сколько краски пойдёт на окраску пола длиной 8 м и шириной 6 м, если на окраску 1 кв. м требуется 150 г краски?

Числа и цифры

Числа — это единицы счета. С помощью чисел можно сосчитать количество предметов и определить различные величины.

Для записи чисел используются специальные знаки — цифры. Всего их десять: 1, 2, 3, 4, 5, 6, 7, 8, 9, 0.

Натуральные числа — это числа, которые мы используем при счете. Вот они: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, …

• Единица (1) — самое маленькое число, а самого большого числа не существует.
• Ноль (0) означает, что предмета нет. Ноль не является натуральным числом.

От количества цифр в числе зависит его название.

Число, которое состоит из одного знака, называется однозначным. Наименьшее однозначное — 1, наибольшее — 9.

Число, которое состоит из двух знаков цифр, называется двузначным. Наименьшее двузначное — 10, наибольшее — 99.

Числа, которые записаны с помощью двух, трех, четырех и более цифр, называются двузначными, трехзначными, четырехзначными или многозначными. Наименьшее трехзначное — 100, наибольшее — 999.

Каждая цифра в записи многозначного числа занимает определенное место — позицию.

Порядок вычисления в выражениях со степенями, корнями, логарифмами и иными функциями

Если у нас в условии стоит выражение со степенью, корнем, логарифмом  или тригонометрической функцией (синусом, косинусом, тангенсом и котангенсом) или иными функциями, то первым делом мы вычисляем значение функции. После этого мы действуем по правилам, указанным в предыдущих пунктах

Иначе говоря, функции по степени важности приравниваются к выражению, заключенному в скобки

Разберем пример такого вычисления.

Пример 6

Условие: найдите, сколько будет (3+1)·2+623−7.

Решение

У нас есть выражение со степенью, значение которого надо найти в первую очередь. Считаем: 62=36. Теперь подставим результат в выражение, после чего оно примет вид (3+1)·2+363−7.

Дальше действуем по знакомому алгоритму: считаем, сколько у нас получится в скобках, потом в оставшемся выражении выполняем умножение и деление, а следом – сложение и вычитание.

(3+1)·2+363−7=4·2+363−7=8+12−7=13

Ответ: (3+1)·2+623−7=13.

В отдельной статье, посвященной вычислению значений выражений, мы приводим и другие, более сложные примеры подсчетов в случае выражений с корнями, степенью и др. Рекомендуем вам с ней ознакомиться.

Всё ещё сложно?
Наши эксперты помогут разобраться

Все услуги

Решение задач

от 1 дня / от 150 р.

Курсовая работа

от 5 дней / от 1800 р.

Реферат

от 1 дня / от 700 р.

Задачи на противоположное движение

1. От одного улья одновременно в противоположных направлениях вылетели две пчелы со скоростью 7 м/с и 6 м/с. Какое расстояние будет между ними через 45 с?2. От одной пристани одновременно в противоположных направлениях вышли два катера со скоростью 32 км/ч и 38 км/ч. Какое расстояние будет между ними через 7 ч?3. С лыжной базы одновременно в противоположных направлениях вышли два лыжника. Через 2 ч расстояние между ними было 60 км. Чему равна скорость второго лыжника, если скорость первого 14 км/ч?4. Из гаража одновременно в противоположных направлениях вышли две автомашины. Одна шла со скоростью 50 км/ч. Через 4 ч расстояние между ними было 480 км. Чему равна скорость второй автомашины?5. С одного аэродрома одновременно в противоположных направлениях вылетели самолёт и вертолёт. Скорость вертолёта 230 км/ч. Через 5 ч расстояние между ними было 4250 км. Найди скорость самолёта.6. Из одного места одновременно в противоположных направлениях вылетели два комара. Через 25 с расстояние между ними было 1850 см. Найди скорость одного из комаров, если скорость другого 38 см/с?7. Из одного города одновременно в противоположных направлениях выехали два автобуса. Через 3 ч расстояние между ними было 243 км. Чему равна скорость первого автобуса, если скорость второго 45 км/ч?8. Из одного укрытия одновременно в противоположных направлениях поплыли две морские змеи. Через 13 мин расстояние между ними было 1066 м. Найди скорость одной из морских змей, если скорость другой 40 м/мин?9. Из одного посёлка одновременно в противоположных направлениях выехали автомобиль и автобус. Через 2 ч расстояние между ними было 310 км. Найди скорость автомобиля, если скорость автобуса 65 км/ч.10. С аэродрома вылетели в одно и то же время в противоположных направлениях два самолёта. Один из них летел со скоростью 640 км/ч, а другой со скоростью 570 км/ч. Какое расстояние будет между ними через 3 ч?

Другие случаи делимости на 4

Рассмотрим случаи, когда нам нужно установить делимость на 4 целого числа, заданного некоторым выражением, значение которого надо вычислить. Для этого мы можем пойти следующим путем:

• представить исходное выражение в виде  произведения нескольких множителей, один из которых будет делиться на 4;
• сделать вывод на основании свойства делимости о том, что все исходное выражение делится на4.

Помочь в решении задачи часто помогает формула бинома Ньютона.

Пример 3

Делится ли на 4 значение выражения 9n-12n+7 при некотором натуральном n?

Решение

Мы можем представить 9 в виде суммы 8+1. Это дает нам возможность применить формулу бинома Ньютона:

9n-12n+7=8+1n-12n+7==Cn·8n+Cn1·8n-1·1+…+Cnn-2·82·1n-2+Cnn-1·8·1n-1+Cnn·1n—12n+7==8n+Cn1·8n-1·1+…+Cnn-2·82+n·8+1—12n+7==8n+Cn1·8n-1·1+…+Cnn-2·82-4n+8==4·2·8n-1+2·Cn1·8n-2+…+2·Cnn-2·81-n+2

Произведение, которое мы получили в ходе преобразований, содержит множитель 4, а выражение в скобках представляет собой натуральное число. Это значит, что это произведение можно разделить на 4 без остатка.

Мы можем утверждать, что исходное выражение 9n-12n+7 делится на 4 при любом натуральном n.

Ответ: Да.

Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!

Описать задание

Также мы можем применить к решению задачи метод математической индукции

Чтобы не отвлекать ваше внимание на второстепенные детали разбора решения, возьмем прежний пример

Пример 4

Докажите, что 9n-12n+7 делится на 4 при любом натуральном n.

Решение

Начнем с установления того, что при значении n=1 значение выражения 9n-12n+7
можно будет разделить на 4 без остатка.

Получаем: 91-12·1+7=4. 4 делится на 4 без остатка.

Теперь мы можем предположить, что при значении n=k значение выражения9n-12n+7 будет делиться на 4. Фактически, мы будем работать с выражением 9k-12k+7, которое должно делиться на 4.

Нам необходимо доказать, что 9n-12n+7 при n=k+1будет делиться на 4 с учетом того, что 9k-12k+7​​​​​ делится на 4:

9k+1-12(k+1)+7=9·9k-12k-5=9·9k-12k+7+96k-68==9·9k-12k+7+4·24k-17

Мы получили сумму, в которой первое слагаемое 9·9k-12k+7 делится на 4 в связи с нашим предположением о том, что 9k-12k+7 делится на 4, а второе слагаемое 4·24k-17 содержит множитель 4, в связи с чем также делится на 4. Это значит, что вся сумма делится на 4.

Ответ: мы доказали, что 9n-12n+7 делится на 4 при любом натуральном значении n методом математической индукции.

Мы можем использовать еще один подход для того, чтобы доказать делимость некоторого выражения на 4. Этот подход предполагает:

• доказательство факта того, что значение данного выражения с переменной n делится на 4 при n=4·m, n=4·m+1, n=4·m+2 и n=4·m+3, где m – целое число;
• вывод о доказанности делимости данного выражения на 4 для любого целого числа n.

Пример 5

Докажите, что значение выражения n·n2+1·n+3·n2+4 при любом целом nделится на 4.

Решение

Если предположить, что n=4·m, получаем:

 4m·4m2+1·4m+3·4m2+4=4m·16m2+1·4m+3·4·4m2+1

Полученное произведение содержит множитель 4, все остальные множители представлены целыми числами. Это дает нам основание предполагать, что все произведение делится на 4.

Если предположить, что n=4·m+1, получаем:

4m+1·4m+12+1·4m+1+3·4m+12+4==(4m·1)+4m+12+1·4m+1·4m+12+4

И опять в произведении, которое мы получили в ходе преобразований,
содержится множитель 4.

Это значит, что выражение делится на 4.

Если предположить, что n=4·m+2, то:

4m+2·4m+22+1·4m+2+3·4m+22+4==2·2m+1·16m2+16m+5·(4m+5)·8·(2m2+2m+1)

Здесь в произведении мы получили множитель 8, который можно без остатка поделить на 4. Это значит, что все произведение делится на 4.

Если предположить, что n=4·m+3, получаем:

4m+3·4m+32+1·4m+3+3·4m+32+4==4m+3·2·8m2+12m+5·2·2m+3·16m2+24m+13==4·4m+3·8m2+12m+5·16m2+24m+13

Произведение содержит множитель 4, значит делится на 4 без остатка.

Ответ: мы доказали, что исходное выражение делится на 4 при любом n.

Всё ещё сложно?
Наши эксперты помогут разобраться

Все услуги

Решение задач

от 1 дня / от 150 р.

Курсовая работа

от 5 дней / от 1800 р.

Реферат

от 1 дня / от 700 р.

Порядок вычислений в выражениях со скобками

Иногда выражения могут содержать скобки, которые подсказывают порядок выполнения математических действий. В этом случае правило звучит так:

Сначала выполнить действия в скобках, при этом также по порядку слева направо выполняется умножение и деление, затем — сложение и вычитание.

Выражения в скобках рассматриваются как составные части исходного выражения. В них сохраняется уже известный нам порядок выполнения действий.

Рассмотрим порядок выполнения действий на примерах со скобками.

Пример 1. Вычислить: 10 + (8 — 2 * 3) * (12 — 4) : 2.

Как правильно решить пример:

Выражение содержит скобки, поэтому сначала выполним действия в выражениях, которые заключены в эти скобки.

Начнем с первого 8 — 2 * 3. Что сначала, умножение или вычитание? Мы уже знаем правильный ответ: умножение, затем вычитание. Получается так:

8 — 2 * 3 = 8 — 6 = 2.

Переходим ко второму выражению в скобках 12 — 4. Здесь только одно действие – вычитание, выполняем: 12 — 4 = 8.

Подставляем полученные значения в исходное выражение:

10 + (8 — 2 * 3) * (12 — 4) : 2 = 10 + 2 * 8 : 2.

Порядок действий: умножение, деление, и только потом — сложение. Получится:

10 + 2 * 8 : 2 = 10 + 16 : 2 = 10 + 8 = 18.

На этом все действия выполнены.

Ответ: 10 + (8 — 2 * 3) * (12 — 4) : 2 = 18.

Можно встретить выражения, которые содержат скобки в скобках. Для их решения, нужно последовательно применять правило выполнения действий в выражениях со скобками. Удобнее всего начинать выполнение действий с внутренних скобок и продвигаться к внешним. Покажем на примере.

Пример 2. Выполнить действия в выражении: 9 + (5 + 1 + 4 * (2 + 3)).

Как решаем:

Перед нами выражение со скобками. Это значит, что выполнение действий нужно начать с выражения в скобках, то есть, с 5 + 1 + 4 * (2 + 3). Но! Это выражение также содержит скобки, поэтому начнем сначала с действий в них:

2 + 3 = 5.

Подставим найденное значение: 5 + 1 + 4 * 5. В этом выражении сначала выполняем умножение, затем — сложение:

5 + 1 + 4 * 5 = 5 + 1 + 20 = 26.

Исходное значение, после подстановки примет вид 9 + 26, и остается лишь выполнить сложение: 9 + 26 = 35.

Ответ: 9 + (5 + 1 + 4 * (2 + 3)) = 35.

Примеры для устного счёта 4 класс

53+47:2-41х3	56:8х10-16:6
74-66х4+48:8	89-68:7х9+78
94-87х3-15:6	4х7+28:8х9
9х5-39х4+36	72:8х6+27:9
40:5+79-69:3	63:9+25:8х20
85-37:4х5+58	8х9-16:7х6
6х5х3-72:2	100-46:9х7+39
100-73:3х5+47	7х9-39:8х30
93-58:5х3+79	4х9+18:6+87
40х2-56:4х3	6х8+33:9х8
17+15:4+67+25	80-35:9х7+65
7х1+86-79:7	63:7х8-36:9
4х8+17:7+83	100-51:7х9-63
36:6х8+24:9	56:8х6-35:7
2х7+86:20х9	8х7-29:9-3
17+46:7+40-37	72:9+72:80х8
7х8+25:9+91	17+64:9х6-29
6х4+48:8х9	32:8х6+48:9
9х7-27:6х8	6х9-26:7х9
3х9+45:8+71	93-58:7х9+55
100-37:9х7+25	27:3+89-69х2
43+29:9х6+46	36:4х5-28+14
21:3х2+67-39	9х2:3+89-14
7х5-19+74:9	9х3+56-37:2
25:5х20-33+9	24:3х5х2-47
45:5х4+59-17	40:8х4+76-25
8х1+75-26:3	18:3х4+76-66
6х4+49-35:19	6х3+47-29:9
20:4х8-23+41	14:2х5+58-61
9х4-19+46:21	7х3+69-73х2
28:4х5+39-55	7х4+72-56:11
8х3:4+75-24	32:4+67-49х3
35:5+65-58х4	6х3:2+46-37
3х7+69-65:5	56:7х9-43+17
9х6-19+49:4	54:9х6+57-19
20:5х6+56:20	15:5х3+21-17

Задачи на движение в обратном направлении

1. Расстояние между городами 504 км. Сколько времени потребуется машине на проезд туда и обратно, если скорость машины в одном направлении 63 км/ч, а в обратном на 21 км/ч больше?2. Расстояние между пристанями в 40 км лодка прошла за 5 ч. На обратном пути её скорость увеличилась на 2 км/ч. За какое время лодка пройдёт весь путь туда и обратно?3. Мальчики прошли до деревни 30 км, двигаясь со скоростью 5 км/ч, а обратно они ехали на велосипеде в 2 раза быстрее. За сколько часов они проехали это расстояние?4. Расстояние между двумя пристанями 45 км. Катамаран прошёл его за 3 ч, на обратном пути его скорость уменьшилась на 6 км/ч. Сколько времени катамаран потратил на путь туда и обратно?5. Расстояние между пристанями 480 км. Катер «Метеор» прошёл его за 6 ч. На обратном пути его скорость увеличилась на 16 км/ч. За какое время катер «Метеор» пройдёт весь путь туда и обратно?6. Божья коровка пролетела до места приземления 3 мин со скоростью 80 см/мин. После этого ей осталось пролететь в 2 раза меньше, и на этот путь она потратила 2 мин. С какой скоростью полетела божья коровка оставшийся путь?7. Путь от города до посёлка, равный 60 км, велосипедист проехал за 4 ч. На обратном пути он уменьшил скорость на 5 км/ч. Сколько времени велосипедист потратил на путь туда и обратно?8. Расстояние между пристанями в 200 км теплоход прошёл за 5 ч. На обратном пути его скорость уменьшилась в 2 раза. За какое время теплоход пройдёт весь путь туда и обратно?9. Баржа проплыла против течения расстояние 84 км за 7 ч, а на обратном пути её скорость увеличилась на 9 км/ч. Сколько времени она потратила на путь туда и обратно?10. Машина шла до остановки 5 ч со скоростью 68 км/ч. После этого ей осталось проехать вдвое меньший путь, на который она потратила 2 ч. С какой скоростью ехала машина после остановки?

Задачи на движение в одном направлении

1. Моторная лодка, двигаясь со скоростью 25 км/ч, прошла путь между пристанями за 2 ч. Сколько потребуется времени, чтобы пройти этот же путь на байдарке, если она движется со скоростью 5 км/ч?2. Ворона летела 3 ч со скоростью 50 км/ч. Сколько потребуется времени скворцу, чтобы пролететь это же расстояние со скоростью 75 км/ч?3. Пешеход шёл со скоростью 6 км/ч и был в пути 6 ч. Сколько времени понадобится, чтобы пройти такое же расстояние лыжнику, скорость которого 12 км/ч?4. Чёрный стриж, двигаясь со скоростью 120 км/ч, был в пути 2 ч. Сколько потребуется времени галке, чтобы пролететь это же расстояние со скоростью 60 км/ч?5. Машина «скорой помощи», двигаясь со скоростью 120 км/ч, была в пути 2 ч. Сколько потребуется времени автомобилю «Запорожец», чтобы проехать этот же путь со скоростью 60 км/ч?6. Гепард пробежал 3 ч со скоростью 100 км/ч. Сколько потребуется времени слону, чтобы пробежать это же расстояние, если его скорость равна 50 км/ч?7. Вёсельная лодка, двигаясь со скоростью 5 км/ч, была в пути 6 ч. За какое время можно проплыть этот путь на катамаране со скоростью 15 км/ч?8. Путь между двумя деревнями мальчик проходит за 5 ч со скоростью 4 км/ч. За какое время он проезжает этот путь на велосипеде со скоростью 10 км/ч?9. Эскимосская собака бежала 60 с со скоростью 15 м/с. За какое время может пробежать этот путь гончая собака, двигаясь со скоростью 30 м/с?10. Рыба-меч, двигаясь со скоростью 70 км/ч, была в пути 2 ч. За какое время может проплыть этот путь скумбрия, двигаясь со скоростью 20 км/ч?

Описание

Программа «Задание на неделю 4 класс» формирует задачи и примеры по математике, которые помогут закрепить ребенку все знания, полученные в четвертом классе в течение года, а также подготовится к проверочной и контрольной работе.

На листе формата А4 формируется 13 заданий по математике. При этом задания даются в небольшом объеме, но с максимальным охватом всех типов примеров. Это позволяет детям быстро вспомнить материал 4 класса.

В каждую карточку входят следующие виды заданий:

• чередующиеся задания, включающее:
  • • задание на повторение понятий «сумма», «разность», «произведение» и «частное» с вычислениями;
    • примеры на нахождение сторон, периметра и площади прямоугольника;
    • простые задачи на движение: нахождение скорости, времени или расстояния.
• примеры на сложение, вычитание, умножение и деление, в том числе: логические (вставить знаки для получения верного равенства),
• выражения на порядок действий (от пяти действий со скобками);
• примеры на умножение и деление разных типов: умножение и деление круглых чисел, внетабличное умножение и деление;
• примеры на деление с остатком с вычисление частного, уменьшаемого или вычитаемого;
• решение уравнений;
• задание на сравнение дробей (долей)
• задание на нахождение части от числа (от суммы, разности, произведения или частного);
• задания на повторение единиц измерения длины, массы и времени;
• задание на нахождение доли и процентов от единиц измерения: длины, площади, массы и времени;
• примеры в столбик: сложение трехзначных чисел, вычитание трехзначных чисел, умножение двухзначного числа на однозначное, умножение трехзначного числа на однозначное и двузначное, на однозначное число.

Программа «Задание на неделю 4 класс» написана в Excel с помощью макросов. Данные генерируются случайным образом, что позволяет получить более тысячи вариантов заданий для 4 класса, карточки заданий не повторяются.

Для ознакомления с программой можно скачать изображение карточки, которая получилась с помощью программы. Для получения новой карточки математического диктанта достаточно скачать, нажать на кнопку и распечатать.

Другие программы, которые помогут закрепить навыки счета:

• Цепочки примеров в пределах 1000 (все действия)
• Числовые пирамиды большие (в пределах 50,100 и больше)
• Умножение и деление по типам (табличное, внетабличное, круглых чисел)
• Сложение и вычитание в столбик
• Умножение и деление в столбик
• Деление с остатком на число (с выбором уровня сложности)
• Порядок действий в пределах 1000 (все действия)
• Сложные примеры на порядок действий
• Выражения с именованными числами

Основные операции в математике

Основные операции, которые используют в математике — это сложение, вычитание, умножение и деление. Помимо этих операций есть ещё операции отношения, такие как равно (=), больше (>), меньше (<), больше или равно (≥), меньше или равно (≤), не равно (≠).

Операции действия:

• сложение (+)
• вычитание (-)
• умножение (*)
• деление (:)

Операции отношения:

• равно (=)
• больше (>)
• меньше (<)
• больше или равно (≥)
• меньше или равно (≤)
• не равно (≠)

Сложение — операция, которая позволяет объединить два слагаемых.

Запись сложения: 5 + 1 = 6, где 5 и 1 — слагаемые, 6 — сумма.

Вычитание — действие, обратное сложению.

Запись вычитания: 10 — 1 = 9, где 10 — уменьшаемое, 1 — вычитаемое, 9 — разность.

Если разность 9, сложить с вычитаемым 1, то получится уменьшаемое 10. Операция сложения 9 + 1 = 10 является контрольной проверкой вычитания 10 — 1 = 9.

Умножение — арифметическое действие в виде краткой записи суммы одинаковых слагаемых.

• Запись: 3 * 4 = 12, где 3 — множимое, 4 — множитель, 12 — произведение.
• 3 * 4 = 3 + 3 + 3 + 3

В случае, если множимое и множитель поменять ролями, произведение остается одним и тем же. Например: 5 * 2 = 5 + 5 = 10.

Поэтому и множитель, и множимое называют сомножителями.

Деление — арифметическое действие обратное умножению.

Запись: 30 : 6 = 5 или 30/6 = 5, где 30 — делимое, 6 — делитель, 5 — частное.

В этом случае произведение делителя 6 и частного 5, в качестве проверки, дает делимое 30.

Если в результате операции деления, частное является не целым числом, то его можно представить в виде дроби.

Возведение степень — операция умножения числа на самого себя несколько раз.

Основание степени — число, которое повторяется сомножителем определённое количество раз.

Показатель степени — число, которое указывает, сколько раз берется одинаковый множитель.

Степенью называется число, которое получается в результате взаимодействия основания и показателя степени.

• Запись: 34 = 81, где 3 — основание степени, 4 — показатель степени, 81 — степень.
• 3^4 = 3 * 3 * 3 * 3

Вторая степень называется квадратом, третья степень — кубом. Первой степенью числа называют само это число.

Извлечение корня — арифметическое действие, обратное возведению в степень.

• Запись: 4√81 = 3, где 81 — подкоренное число, 4 — показатель корня, 3 — корень.
• З^4 = 81 — возведение числа 3 в четвертую степень дает 81 (проверка извлечения корня).
• 2√16 = 4 — корень второй степени называется — квадратным.

При знаке квадратного корня показатель корня принято опускать: √16 = 4.

3√8 = 2 — корень третьей степени называется — кубическим.

Сложение и вычитание, умножение и деление, возведение в степень и извлечение корня попарно представляют обратные друг другу действия. Далее узнаем порядок выполнения арифметических действий.

Потренируемся

Пример 1. Записать цифрами число, в котором содержится:

1. 55 единиц второго класса и 100 единиц первого класса;
2. 110 единиц второго класса и 5 единиц первого класса;
3. 7 единиц второго класса и 13 единиц первого класса.

Ответ:

1. 55 100;
2. 110 005;
3. 7 013.

Все разрядные единицы, кроме простых единиц, называют составными единицами. Каждые десять единиц любого разряда составляют одну единицу следующего более высокого разряда:

• 10 единиц равны 1 десятку;
• 10 десятков равны 1 сотне;
• 10 сотен равны 1 тысяче;
• 10 тысяч равны 1 десятку тысяч;
• 10 десятков тысяч равны 1 сотне тысяч;
• 10 сотен тысяч равны 1 миллиону.

Чтобы узнать, сколько в числе заключается всех единиц какого-либо разряда, нужно отбросить все цифры, обозначающие единицы низших разрядов и прочитать число, которое выражено оставшимися цифрами.

Пример 2. Сколько сотен содержится в числе 6284?

Как рассуждаем:

В числе 6284 на третьем месте в классе единиц стоит цифра 2, значит, в числе есть две сотни.

Следующая цифра слева — 6, означает тысячи. Так как в каждой тысяче содержится 10 сотен то, в 6 тысячах их заключается 60.

Значит, в данном числе содержится 62 сотни.

Цифра 0 в любом разряде означает отсутствие единиц в данном разряде.

Проще говоря, цифра 0 в разряде десятков означает отсутствие десятков, в разряде сотен — отсутствие сотен и т. д. В том разряде, где стоит 0, при чтении числа ничего не произносится:

• 11 627 — одиннадцать тысяч шестьсот двадцать семь.
• 31 502 — тридцать одна тысяча пятьсот два.

Чтобы проще освоить эту тему, можно распечатать таблицу классов и разрядов для учащихся 4 класса и обращаться к ней, если возникнут сложности.

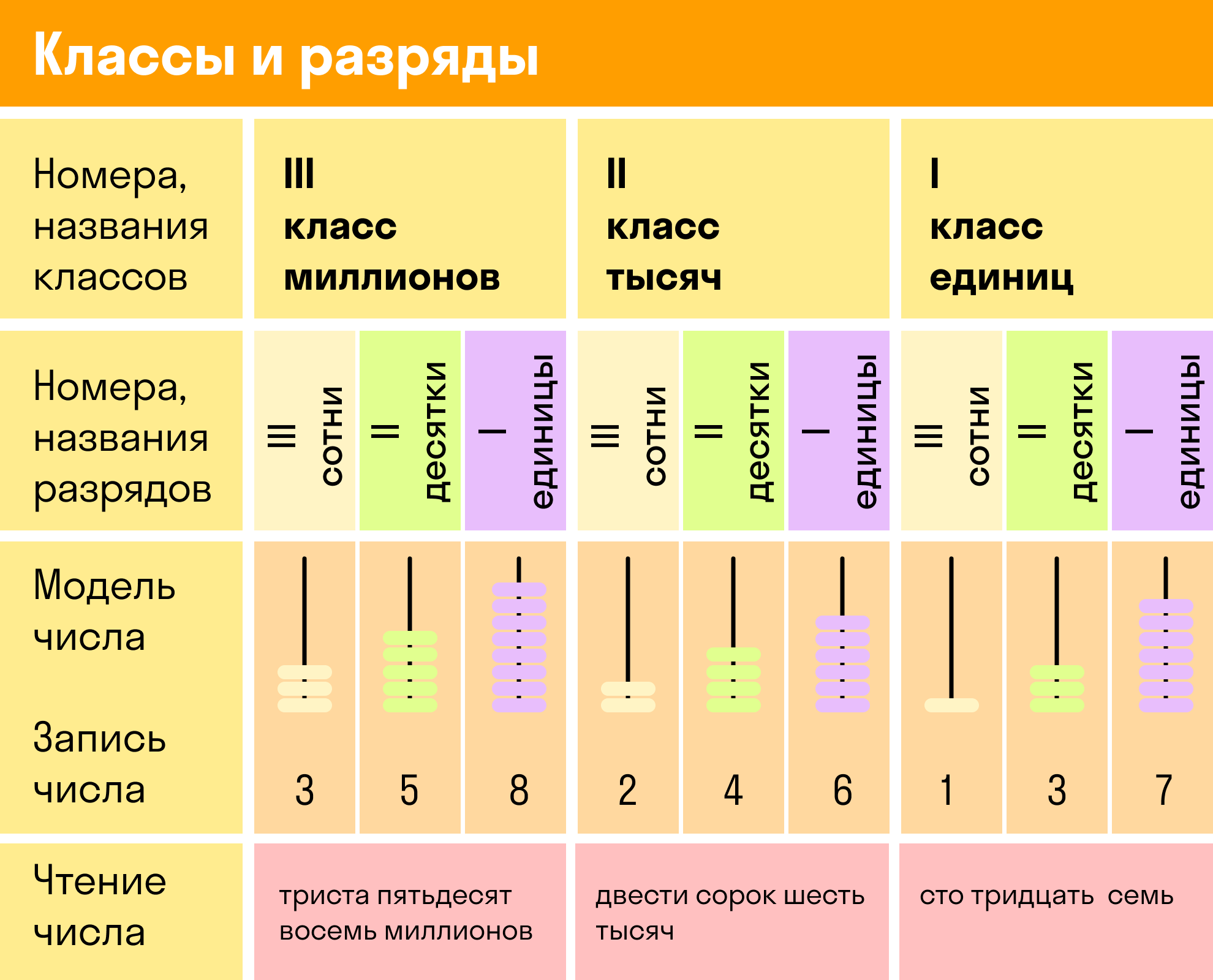
Задачи на нахождение неизвестного по двум разностям

1. 480 кг черешни и 870 кг вишни рассыпали в ящики по одинаковому количеству килограммов. Вишни получилось на 26 ящиков больше, чем черешни. Сколько ящиков вишни и сколько черешни получилось?2. Два грузовика возили из карьера песок и сделали одинаковое количество рейсов. Один возил по 5 т песка за рейс, а другой — по 3 т. Всего первый грузовик перевёз на 18 т песка больше, чем второй. Сколько тонн песка перевёз каждый грузовик?3. Два автобуса вышли из двух городов навстречу друг другу с одинаковой скоростью и встретились через 8 ч после выхода второго поезда. Первый поезд вы ехал на 3 ч раньше и проехал на 183 км больше. Каково расстояние между городами?4. По одной дороге из города в деревню можно доехать за 2 ч. По другой с той же скоростью за 6 ч, так как вторая дорога на 96 км длиннее. Чему равна длина каждой дороги?5. На нефтезавод пришли два поезда с цистернами нефти. Первый поезд привёз 46 цистерн нефти, а другой — 28 цистерн. Второй поезд привёз на 180 т меньше, чем первый. Сколько тонн нефти привёз каждый поезд?6. В январе кроликам дали на 16 кг комбикорма больше, чем в феврале. Сколько килограммов комбикорма расходовали в каждом месяце? (В марте 31 день, в феврале 28 дней.)7. В одном мотке 115 м провода. В другом 70 м такого же провода. Первый моток на 1350 руб. дороже. Сколько стоит весь провод?8. Один комбайн убирал хлеб в поле 6 дней, а другой 9 дней. Первый комбайн собрал на 87 т зерна меньше. Сколько тонн зерна собрал каждый комбайн?9. Собрали несколько ящиков слив и столько же ящиков вишни. Каждый ящик со сливами весит на 4 кг больше, чем ящик с вишнями. Всего сливы было собран на 28 кг больше, чем вишни. Сколько всего ящиков сливы и вишни собрали?10. В ресторане в первом зале 24 одинаковых стола, а во втором 15 таких же столов. Сколько мест за каждым столом, если в первом зале на 36 мест больше, чем во втором зале?

Разряды чисел

От позиции, на которой стоит цифра в записи числа, зависит ее значение. Например:

1 123 содержит в себе: 3 единицы, 2 десятка, 1 сотню, 1 тысячу.

Можно сформулировать иначе и сказать, что в заданном числе 1 123 цифра 3 располагается в разряде единиц, 2 в разряде десятков, 1 в разряде сотен, а 1 служит значением разряда тысяч.

Проясним, что такое разряд в математике. Разряд — это позиция или место расположения цифры в записи натурального числа.

У каждого разряда есть свое название. Слева всегда живут старшие разряды, а справа — младшие. Чтобы быстрее запомнить, можно использовать таблицу.

Количество разрядов всегда соответствует количеству знаков в числе. В этой таблице есть названия всех разрядов для числа, которое состоит из 15 знаков. У следующих разрядов также есть названия, но они используются крайне редко.

Низший (младший) разряд многозначного натурального числа — разряд единиц.

Высший (старший) разряд многозначного натурального числа — разряд, соответствующий крайней левой цифре в заданном числе.

Вы наверняка заметили, что в учебниках часто ставят небольшие пробелы при записи многозначных чисел. Так делают, чтобы натуральные числа было удобно читать. А еще чтобы визуально разделить классы чисел.

Разрядные единицы обозначают так:

• Единицы — единицами первого разряда (или простыми единицами) и пишут на первом месте справа.
• Десятки — единицами второго разряда и записывают в числе на втором месте справа.
• Сотни — единицами третьего разряда и записывают на третьем месте справа.
• Единицы тысяч — единицами четвертого разряда и записывают на четвертом месте справа.
• Десятки тысяч — единицами пятого разряда и записывают на пятом месте справа.
• Сотни тысяч — единицами шестого разряда и записывают в числе на шестом месте справа и так далее.

Каждые три разряда, следующие друг за другом, составляют класс. Первые три разряда: единицы десятки и сотни — образуют класс единиц (первый класс). Следующие три разряда: единицы тысяч, десятки тысяч и сотни тысяч — образуют класс тысяч (второй класс). Третий класс будут составлять единицы, десятки и тысячи миллионов и так далее.

Чтобы легче понимать математику — записывайтесь на наши онлайн-курсы по математике!

Задание 2:

Сложная задача по математике для 4 класса: Из двух городов по реке одновременно выплыли навстречу друг другу две моторные лодки. Скорость первой лодки 15км/ч, второй лодки 35км/ч. Первая лодка двигалась по течению реки. Скорость течения реки 5км/ч. Через сколько часов лодки встретились, если расстояние между городами 250км?

Решение:

Пусть до встречи лодок первая проплыла x км. Тогда вторая лодка проплыла (250 — x) км. Учитывая скорость течения реки, скорость первой лодки 15 + 5 = 20км/ч. Соответственно, скорость второй лодки 35 — 5 = 30км/ч. Очевидно, что время в пути до встречи одинаково, поэтому можно записать уравнение: x/20 = (250 — x)/30; x * 30 = 20 * (250 — x); 30x = 5000 — 20x; 50x = 5000; x = 100км.

Первая лодка до встречи со второй прошла 100км. Рассчитаем время: t = x/20 = 100/20 = 5ч.

Для проверки мы можем рассчитать время второй лодки: t = x/20 = (250 — x)/30 = 150/30 = 5ч. Ответ: лодки встретились через 5 часов.

Примеры линейных уравнений

Теперь мы знаем, как решать линейные уравнения. Осталось попрактиковаться на задачках, чтобы чувствовать себя увереннее на контрольных. Давайте решать вместе!

Пример 1. Как правильно решить уравнение: 6х + 1 = 19.

Решаем так:

1. Перенести 1 из левой части в правую со знаком минус.

   6х = 19 — 1

2. Выполнить вычитание.

   6х = 18

3. Разделить обе части на общий множитель, то есть 6.

   х = 2

Ответ: х = 2.

Пример 2. Как решить уравнение: 5(х — 3) + 2 = 3 (х — 4) + 2х — 1.

Решаем так:

1. Раскрыть скобки

   5х — 15 + 2 = 3х — 2 + 2х — 1

2. Сгруппировать в левой части члены с неизвестными, а в правой — свободные члены.

   5х — 3х — 2х = — 12 — 1 + 15 — 2

3. Приведем подобные члены.

   0х = 0

Ответ: х — любое число.

Пример 3. Решить: 4х = 1/8.

Решаем так:

1. Найти неизвестную переменную.

   х = 1/8 : 4

   х = 1/12

Ответ: 1/12 или 0,83. О десятичных дробях можно почитать здесь.

Пример 4. Решить: 4(х + 2) = 6 — 7х.

Решаем так:

1. 4х + 8 = 6 — 7х
2. 4х + 7х = 6 — 8
3. 11х = −2
4. х = −2 : 11
5. х = — 0, 18

Ответ: — 0,18.

Пример 5. Решить:

Решаем так:

1. 3(3х — 4) = 4 · 7х + 24
2. 9х — 12 = 28х + 24
3. 9х — 28х = 24 + 12
4. -19х = 36
5. х = 36 : (-19)
6. х = — 36/19

Ответ: 1 17/19.

Пример 6. Как решить линейное уравнение: х + 7 = х + 4.

Решаем так:

1. Раскрыть скобки

   5х — 15 + 2 = 3х — 2 + 2х — 1

2. Сгруппировать в левой части неизвестные члены, в правой — свободные члены:

   х — х = 4 — 7

3. Приведем подобные члены.

   0 * х = — 3

Ответ: нет решений.

Пример 7. Решить: 2(х + 3) = 5 — 7х..

Решаем так:

1. 2х + 6 = 5 — 7х
2. 2х + 6х = 5 — 7
3. 8х = −2
4. х = −2 : 8
5. х = — 0,25

Ответ: — 0,25.