Уравнения 2 класс по математике

Задачи по математике для 2 класса.

Задачи на 2 действия.

Задача 1

Сеня должен прочитать 9 литературных произведений. После того как он прочитал несколько, ему осталось прочитать 3 рассказа и 1 сказку. Сколько литературных произведений прочитал Сеня?

Задача 2

У Лёни было 19 ручек. За первое полугодие он исписал 3 ручки. Сколько ручек он исписал за второе полугодие, если к концу года у него осталось 11 ручек?

Задача 5

У Кости было 20 солдатиков. Он подарил несколько солдатиков другу, и у него осталось 4 пехотинца и 5 конников. Сколько солдатиков Костя подарил другу?

Задача 6

На полке стояло 13 тарелок и 5 блюдец. Несколько предметов взяли. Сколько предметов взяли, если осталось 8 тарелок и блюдец?

Задача 9

В троллейбусе ехали 12 человек. Когда в троллейбус вошли 3 мужчины и несколько женщин, в нём стало 19 человек. Сколько женщин вошли в троллейбус?

Задача 10

Катя купила 9 ручек. После того как она отдала несколько ручек сестре, у неё осталось 4 синие ручки и 2 чёрные. Сколько ручек Катя отдала сестре?

Задача 11

На стене висело 8 фотографий. Убрали 1 чёрно-белую фотографию и несколько цветных. Сколько цветных фотографий убрали, если осталось 5 фотографий?

Задача 13

В папке было 2 листа красной бумаги и 4 листа жёлтой. Когда туда положили несколько листов синей бумаги, всего стало 10 листов. Сколько листов синей бумаги положили?

Задача 15

Ваня нашёл 17 грибов. После того как несколько грибов поджарили, осталось 3 подберёзовика и 4 белых. Сколько грибов поджарили?

Задача 16

На диване лежало 2 красные подушки и столько же зелёных. Когда положили ещё несколько белых, всего подушек стало 8. Сколько белых подушек положили?

Задача 17

Маша испекла 18 пирожков. К ней на чай пришли подруги, и после чаепития у неё осталось 3 пирожка с вареньем и 1 пирожок с капустой. Сколько пирожков съели подруги?

Задача 18

В ящике было 18 кг фруктов. Взяли 5 кг яблок и несколько килограммов груш. Сколько килограммов груш взяли, если в ящике осталось

10 кг фруктов?

Задача 19

На прилавке лежало 5 пачек масла и столько же пачек маргарина. Когда несколько пачек убрали, их осталось 6. Сколько пачек убрали?

Задача 20

В холодильнике было 6 пакетов молока и 1 пакет ряженки. Когда туда поставили несколько пакетов кефира, всего стало 9 пакетов. Сколько пакетов кефира поставили?

Задача 21

В вагоне сидели 6 человек. Вошли ещё 4, а несколько человек вышли. Сколько человек вышли, если в вагоне остались 7 человек?

Задача 22

В палатке продавалось 19 кг овощей. К концу дня осталось 2 кг картофеля и 1 кг моркови. Сколько килограммов овощей продали?

Задача 23

В зале музея было 11 хрустальных ваз и 3 фарфоровые. Принесли ещё несколько ваз, и всего ваз стало 17. Сколько ваз принесли?

Задача 24

На полке лежало 16 полотенец. Взяли 1 вафельное полотенце и несколько махровых. Сколько махровых полотенец взяли, если на полке осталось 13 полотенец?

Задача 25

На столе было 8 ложек. Убрали 2 столовые ложки и несколько десертных. Сколько десертных ложек убрали, если осталось 3 ложки?

Задача 26

На полке лежало 13 синих футболок и 1 серая. Когда положили ещё несколько футболок, всего их стало 18. Сколько футболок положили?

Задача 27

Рома купил 15 тетрадей. После того как он исписал несколько, осталось 2 тетради в клетку и 1 тетрадь в линейку. Сколько тетрадей исписал Рома?

Задача 28

В гараже хранилось 8 велосипедов. Из него взяли 2 взрослых велосипеда и несколько детских. Сколько детских велосипеда взяли, если в гараже остался 1 велосипед?

Задача 29

Даша должна была решить 7 задач. После того как она решила несколько, ей осталось решить 2 задачи на сложение и столько же на вычитание. Сколько задач решила Даша?

На блюде было 17 пирожных. Папа съел 3 пирожных, и мама съела несколько. Сколько пирожных съела мама, если на блюде осталось 12 пи-рожных?

Понятие квадратного уравнения

Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.

Например, возьмем выражение 8 + 4 = 12. При вычислении левой части получается верное числовое равенство, то есть 12 = 12.

Уравнением можно назвать выражение 8 + x = 12, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.

Степень уравнения можно определить по наибольшей степени, в которой стоит неизвестное. Если неизвестное стоит во второй степени, значит, такое уравнение является квадратным.

Квадратное уравнение — это ax2 + bx + c = 0, где a — первый или старший коэффициент, не равный нулю, b — второй коэффициент, c — свободный член.

Есть три вида квадратных уравнений:

• не имеют корней;
• имеют один корень;
• имеют два различных корня.

Понятие квадратного уравнения

Уравнения — это математическое равенство, в котором неизвестна одна или несколько величин. Значения неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.

Например, возьмем выражение 3 + 4 = 7. При вычислении левой части получается верное числовое равенство, то есть 7 = 7.

Уравнением можно назвать выражение 3 + x = 7, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.

Степень уравнения можно определить по наибольшей степени, в которой стоит неизвестное. Если неизвестное стоит во второй степени — это квадратное уравнение.

Квадратное уравнение — это ax2 + bx + c = 0, где a — первый или старший коэффициент, не равный нулю, b — второй коэффициент, c — свободный член.

Чтобы запомнить месторасположение коэффициентов, давайте потренируемся определять их.

Есть три вида квадратных уравнений:

• не имеют корней;
• имеют один корень;
• имеют два различных корня.

Чтобы определить, сколько корней имеет уравнение, нужно обратить внимание на дискриминант. Чтобы его найти, берем формулу: D = b2 − 4ac

А вот свойства дискриминанта:

• если D < 0, корней нет;
• если D = 0, есть один корень;
• если D > 0, есть два различных корня.

С этим разобрались. А сейчас посмотрим подробнее на различные виды квадратных уравнений.

Как решать квадратные уравнения через дискриминант

В 8 классе на алгебре можно встретить задачу по поиску действительных корней квадратного уравнения

Для этого важно перед использованием формул найти дискриминант и убедиться, что он неотрицательный. Только после этого вычисляем значения корней

Если дискриминант отрицательный, значит уравнение не имеет действительных корней.

Алгоритм решения квадратного уравнения ax2 + bx + c = 0:

• как найти дискрининант: D = b2 − 4ac;
• если дискриминант отрицательный — зафиксировать, что действительных корней нет;
• если дискриминант равен нулю — вычислить единственный корень уравнения по формуле х = — b2/2a;
• если дискриминант положительный — найти два действительных корня квадратного уравнения по формуле корней

А вот и еще одна табличка: в ней вы найдете формулы для поиска корней квадратных уравнений при помощи дискриминанта:

Чтобы запомнить алгоритм решения квадратных уравнений и с легкостью его использовать, важно практиковаться. Вперед!

Примеры решения квадратных уравнений с помощью дискриминанта

Пример 1. Решить уравнение: 3×2 — 4x + 2 = 0.

Как решаем:

1. Определим коэффициенты: a = 3, b = -4, c = 2.
2. Найдем дискриминант: D = b2 — 4ac = (-4)2 — 4 * 3 * 2 = 16 — 24 = -8.

Ответ: D < 0, корней нет.

Пример 2. Решить уравнение: x2 — 6x + 9 = 0.

Как решаем:

1. Определим коэффициенты: a = 1, b = -6, c = 9.
2. Найдем дискриминант: D = b2 — 4ac = (-6)2 — 4 * 1 * 9 = 36 — 36 = 0.
3. D = 0, значит уравнение имеет один корень:

Ответ: корень уравнения 3.

Пример 3. Решить уравнение: x2 — 4x — 5 = 0.

Как решаем:

1. Определим коэффициенты: a = 1, b = -4, c = -5.
2. Найдем дискриминант: D = b2 — 4ac = (-4)2 — 4 * 1 * (-5) = 16 + 20 = 36.
3. D > 0, значит уравнение имеет два корня:

x₁ = (4 + 6) : 2 = 5,

x₂ = (4 — 6) : 2 = -1.

Ответ: два корня x₁ = 5, x₂ = -1.

Не желаешь повторить формулы сокращенного умножения?

Какие бывают виды уравнений

Уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные.

Особенность преобразований алгебраических уравнений в том, что в левой части должен остаться многочлен от неизвестных, а в правой — нуль.

Линейное уравнение выглядит так	ах + b = 0, где a и b — действительные числа. Что поможет в решении: если а не равно нулю, то у уравнения единственный корень: х = -b : а; если а равно нулю — у уравнения нет корней; если а и b равны нулю, то корень уравнения — любое число.
Квадратное уравнение выглядит так:	ax2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, a ≠ 0.

Система уравнений — это несколько уравнений, для которых нужно найти значения неизвестных. Она имеет вид ax + by + c = 0 и называется линейным уравнением с двумя переменными x и y, где a, b, c — числа.

Решением этого уравнения называют любую пару чисел (x; y), которая соответствует этому выражению и является верным числовым равенством.

Числовой коэффициент — число, которое стоит при неизвестной переменной.

Кроме линейных и квадратных есть и другие виды уравнений, с которыми мы познакомимся в следующий раз:

• кубические
• уравнение четвёртой степени
• иррациональные и рациональные
• системы линейных алгебраических уравнений

Дискриминант: формула корней квадратного уравнения

Чтобы найти результат квадратного уравнения, придумали формулу корней. Выглядит она так:

где D = b2 − 4ac — дискриминант квадратного уравнения.

Эта запись означает:

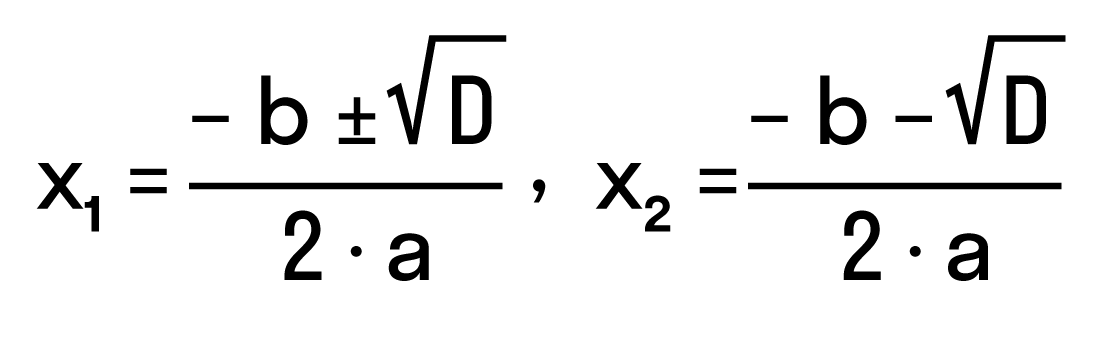
Чтобы легко применять эту формулу, нужно понять, как она получилась. Давайте разбираться.

Выводим формулу корней квадратного уравнения

Продолжим изучать формулу корней квадратного уравнения.

Пусть перед нами есть задача решить квадратное уравнение ax2 + bx + c = 0. Выполним ряд равносильных преобразований:

• разделим обе части этого уравнения на отличное от нуля число a, после чего получим приведенное квадратное уравнение:
• выделим полный квадрат левой части нового уравнения:

  ,

  после чего уравнение примет вид

• перенесем два последних слагаемых в правую часть и сменим знак на противоположный:
• преобразуем выражение в правой части:

Так, мы пришли к уравнению , которое полностью равносильно исходному ax2 + bx + c = 0.

Отсюда выводы про корни уравнения :

И еще один вывод: есть у уравнения корень или нет, зависит от знака выражения в правой части

При этом важно помнить, что знак этого выражения задается знаком числителя. Потому выражение принято называть дискриминантом квадратного уравнения и обозначается буквой D

По значению и знаку дискриминанта можно сделать вывод, есть ли действительные корни у квадратного уравнения, и сколько.

Повторим:

Алгоритм решения квадратных уравнений по формулам корней

Теперь мы знаем, что при решении квадратных уравнения можно использовать универсальную формулу корней — это помогает находить комплексные корни.

В 8 классе на алгебре можно встретить задачу по поиску действительных корней квадратного уравнения

Для этого важно перед использованием формул найти дискриминант и убедиться, что он неотрицательный, и только после этого вычислять значения корней. Если дискриминант отрицательный, значит уравнение не имеет действительных корней

Алгоритм решения квадратного уравнения ax2 + bx + c = 0:

• вычислить его значение дискриминанта по формуле D = b2−4ac;
• если дискриминант отрицательный, зафиксировать, что действительных корней нет;
• если дискриминант равен нулю, вычислить единственный корень уравнения по формуле х = −b/2a;
• если дискриминант положительный, найти два действительных корня квадратного уравнения по формуле корней

Чтобы запомнить алгоритм решения квадратных уравнений и с легкостью его использовать, давайте тренироваться!

Примеры решения квадратных уравнений

Как решать квадратные уравнения мы уже знаем, осталось закрепить знания на практике.

Пример 1. Решить уравнение −4×2 + 28x — 49 = 0.

Как решаем:

1. Найдем дискриминант: D = 282 — 4(-4)(-49) = 784 — 784 = 0
2. Так как дискриминант равен нулю, значит это квадратное уравнение имеет единственный корень
3. Найдем корень

   х = — 28/2(-4)

   х = 3,5

Ответ: единственный корень 3,5.

Пример 2. Решить уравнение 54 — 6×2 = 0.

Как решаем:

1. Произведем равносильные преобразования. Умножим обе части на −1

   54 — 6×2 = 0 | *(-1)

   6×2 — 54 = 0

2. Оставим неизвестное в одной части, остальное перенесем с противоположным знаком в другую

   6×2 = 54

   х2 = 9

   х = ±√9

   х₁ = 3, х₂ = — 3

Ответ: два корня 3 и — 3.

Пример 3. Решить уравнение x2— х = 0.

Как решаем:

1. Преобразуем уравнение так, чтобы появились множители

   х(х — 1) = 0

   х₁ = 0, х₂ = 1

Ответ: два корня 0 и 1.

Пример 4. Решить уравнение x2— 10 = 39.

Как решаем:

1. Оставим неизвестное в одной части, остальное перенесем с противоположным знаком в другую

   x2— 10 = 39

   x2= 39 + 10

   x2= 49

   х = ±√49

   х₁ = 7, х₂ = −7

Ответ: два корня 7 и −7.

Пример 5. Решить уравнение 3×2— 4x+94 = 0.

Как решаем:

1. Найдем дискриминант по формуле

   D = (-4)2 — 4 * 3 * 94 = 16 — 1128 = −1112

2. Дискриминант отрицательный, поэтому корней нет.

Ответ: корней нет.

В школьной программе за 8 класс нет обязательного требования искать комплексные корни, но такой подход может ускорить ход решения. Если дискриминант отрицательный — сразу пишем ответ, что действительных корней нет и не мучаемся.

Как решать простые уравнения

Чтобы научиться решать простые линейные уравнения, нужно запомнить формулу и два основных правила.

1. Правило переноса. При переносе из одной части в другую, член уравнения меняет свой знак на противоположный.

Для примера рассмотрим простейшее уравнение: x+3=5

Начнем с того, что в каждом уравнении есть левая и правая часть.

Перенесем 3 из левой части в правую и меняем знак на противоположный.

Можно проверить: 2 + 3 = 5. Все верно. Корень равен 2.

Решим еще один пример: 6x = 5x + 10.

Как решаем:

1. Перенесем 6x из левой части в правую. Знак меняем на противоположный, то есть минус.

   6x −5x = 10

2. Приведем подобные и завершим решение.

   x = 10

Ответ: x = 10.

2. Правило деления. В любом уравнении можно разделить левую и правую часть на одно и то же число. Это может ускорить процесс решения. Главное — быть внимательным, чтобы не допустить глупых ошибок.

Применим правило при решении примера: 4x=8.

При неизвестной х стоит числовой коэффициент — 4. Их объединяет действие — умножение.

Чтобы решить уравнение, нужно сделать так, чтобы при неизвестной x стояла единица.

Разделим каждую часть на 4. Как это выглядит:

Теперь сократим дроби, которые у нас получились и завершим решение линейного уравнения:

Рассмотрим пример, когда неизвестная переменная стоит со знаком минус: −4x = 12

Как решаем:

1. Сократим обе части на −4, чтобы коэффициент при неизвестной стал равен единице.

   −4x = 12 | :(−4)
   x = −3

Ответ: x = −3.

Если знак минус стоит перед скобками, и по ходу вычислений его убрали — важно не забыть поменять знаки внутри скобок на противоположные. Этот простой факт позволит не допустить обидные ошибки, особенно в старших классах

Напомним, что не у каждого линейного уравнения есть решение — иногда корней просто нет. Изредка среди корней может оказаться ноль — ничего страшного, это не значит, что ход решения оказался неправильным. Ноль — такое же число, как и остальные.

Способов решения линейных уравнений немного, нужно запомнить только один алгоритм, который будет эффективен для любой задачки.

Алгоритм решения простого линейного уравнения
Раскрываем скобки, если они есть. Группируем члены, которые содержат неизвестную переменную в одну часть уравнения, остальные члены — в другую. Приводим подобные члены в каждой части уравнения. Решаем уравнение, которое получилось: aх = b. Делим обе части на коэффициент при неизвестном.

Чтобы быстрее запомнить ход решения и формулу линейного уравнения, скачайте или распечатайте схему-подсказку — храните ее в телефоне, учебники или на рабочем столе.

А вот и видео «Простейшие линейные уравнения» для тех, кто учиться в 5, 6 и 7 классе.

Задачи на умножение-деление в предалах 100.

1. Ученики 1 класса по заданию учительницы взяли в библиотеке по 2 сказки Пушкина. Сколько всего сказок Пушкина выдал библиотекарь второклассникам, если известно, что во втором классе учится 20 человек?

2. Концертный зал имеет 11 рядов, в каждом ряду по 12 кресел. Сколько зрительских мест в этом зале?

3. Чтобы полить одну грядку с огурцами, бабушке нужно 3 л воды. Сколько литров воды потребуется бабушке, чтобы полить 6 таких грядок?

4. В первой банке 12 литров сока. Во второй — в 2 раза меньше. Сколько сока надо перелить из первой банки во вторую, чтобы в обеих банках стало сока поровну? 

5. У белки в дупле заготовлены на зиму  грибы и орехи. Грибов белка заготовила 86 штук, а орехов всего 4 штуки. Во сколько раз больше белка заготовила грибов, чем орехов?

6. Расстояние от глаз телезрителя до экрана телевизора должна быть в 4 раза больше, чем диагональ экрана. каким должно быть это расстояние, если диагональ экрана равна 36 см?

7. Акула за 10 минут проплывает 1 000 м. Какое расстояние она проплывает за 1 минуту?

8. Заяц за час может пробежать 60 км, а волк на 15 км меньше. какое расстояние может пробежать волк за 1 час?

9. Миша каждый день решал по 5 математических задач. Сколько задач Миша решил за неделю?

10. В магазине в понедельник продали 26 сказок Пушкина, а во вторник в 2 раза меньше. Сколько сказок было всего  продано за 2 дня?

Уважаемые читатели!

Все материалы с сайта можно скачивать абсолютно бесплатно. Все материалы проверены антивирусом и не содержат скрытых скриптов.

Материалы в архиве не помечены водяными знаками!

Если материал нарушает чьи-то авторские права, просьба написать нам по обратной связи, указав авторство материала. Мы обязуемся либо убрать материал, либо указать прямую ссылку на автора.

Сайт пополняется материалами на основе бесплатной работы авторов. Eсли вы хотите отблагодарить их за работу и поддержать наш проект, вы можете перевести любую, не обременительную для вас сумму на счет сайта.
Заранее Вам спасибо!!!

Примеры линейных уравнений

Теперь мы знаем, как решать линейные уравнения. Осталось попрактиковаться на задачках, чтобы чувствовать себя увереннее на контрольных. Давайте решать вместе!

Пример 1. Как правильно решить уравнение: 6х + 1 = 19.

Решаем так:

1. Перенести 1 из левой части в правую со знаком минус.

   6х = 19 — 1

2. Выполнить вычитание.

   6х = 18

3. Разделить обе части на общий множитель, то есть 6.

   х = 2

Ответ: х = 2.

Пример 2. Как решить уравнение: 5(х — 3) + 2 = 3 (х — 4) + 2х — 1.

Решаем так:

1. Раскрыть скобки

   5х — 15 + 2 = 3х — 2 + 2х — 1

2. Сгруппировать в левой части члены с неизвестными, а в правой — свободные члены.

   5х — 3х — 2х = — 12 — 1 + 15 — 2

3. Приведем подобные члены.

   0х = 0

Ответ: х — любое число.

Пример 3. Решить: 4х = 1/8.

Решаем так:

1. Найти неизвестную переменную.

   х = 1/8 : 4

   х = 1/12

Ответ: 1/12 или 0,83. О десятичных дробях можно почитать здесь.

Пример 4. Решить: 4(х + 2) = 6 — 7х.

Решаем так:

1. 4х + 8 = 6 — 7х
2. 4х + 7х = 6 — 8
3. 11х = −2
4. х = −2 : 11
5. х = — 0, 18

Ответ: — 0,18.

Пример 5. Решить:

Решаем так:

1. 3(3х — 4) = 4 · 7х + 24
2. 9х — 12 = 28х + 24
3. 9х — 28х = 24 + 12
4. -19х = 36
5. х = 36 : (-19)
6. х = — 36/19

Ответ: 1 17/19.

Пример 6. Как решить линейное уравнение: х + 7 = х + 4.

Решаем так:

1. Раскрыть скобки

   5х — 15 + 2 = 3х — 2 + 2х — 1

2. Сгруппировать в левой части неизвестные члены, в правой — свободные члены:

   х — х = 4 — 7

3. Приведем подобные члены.

   0 * х = — 3

Ответ: нет решений.

Пример 7. Решить: 2(х + 3) = 5 — 7х..

Решаем так:

1. 2х + 6 = 5 — 7х
2. 2х + 6х = 5 — 7
3. 8х = −2
4. х = −2 : 8
5. х = — 0,25

Ответ: — 0,25.

Карточка 2

Сосчитай, записывая примеры в столбик.

32+49	37-16
46+24	70-48
83+8	53-38
38+32	45-8

Сосчитай, записывая примеры в столбик.

80-67	45+14
93-48	38+47
59-42	75+8
36-9	68+27

Сосчитай, записывая примеры в столбик.

46+37	80-38
22+58	93-56
59+9	75-9
64+27	87-32

Карточка 7

В летний лагерь приехали дети на двух автобусах. В первом автобусе было 46 детей, а во втором — на 8 детей меньше. Сколько всего детей приехало в школьный лагерь?

3∙7	2∙9	5∙3	9∙0
20:4	70:10	8∙10	32:4
27:3	21:7	7∙4	8∙3

c∙4=12

6∙c=18

27:c=3

2∙7	5∙9	8∙3	8∙4
25:5	8∙10	7∙0	60:6
36:4	16:4	21:7	15:3

c∙3=12

8∙c=24

25:c=5

2∙7	5∙9	8∙3	8∙4
25:5	8∙10	7∙0	60:6
36:4	16:4	21:7	15:3

c∙3=12

8∙c=24

25:c=5

2∙7	5∙9	8∙3	8∙4
25:5	8∙10	7∙0	60:6
36:4	16:4	21:7	15:3

c∙3=12

8∙c=24

25:c=5

Найди значение выражения, решая по действиям.

60-(8∙3)+(4∙7)

Найди значение выражения, решая по действиям.

70-(7∙3)+(8∙4)

Найди значение выражения, решая по действиям.

64-(27+14)+(6∙4)

Найди значение выражения, решая по действиям.

60-(8∙3)+(4∙7)

Найди значение выражения, решая по действиям.

38+(6∙3)-(4∙7)

Карточка 20

На зиму мама закрыла 4 банки вишнёвого варенья, а малинового — в 3 раза больше. Сколько банок малинового варенья закрыла мама? Сколько всего банок закрыла мама на зиму?

Карточка 21

В первый день маляр покрасил 5 скамеек, а во второй — в 4 раза больше. Сколько скамеек покрасил маляр во второй день? Сколько всего скамеек покрасил маляр за два дня?

Карточка 22

Пятачок за неделю съел 3 баночки мёда, в Винни-Пух — в 3 раза больше. Сколько баночек мёда съел Винни-Пух? Сколько баночек мёда они съели вместе?

Карточка 23

Перед домом посадили 4 ели, а берёз — в 3 раза больше. Сколько посадили берёз? Сколько всего деревьев посадили перед домом?

Карточка 24

Денис нарисовал 16 флажков, а Дима — в 4 раза меньше. Сколько флажков нарисовал Дима? Сколько всего флажков нарисовали мальчики?

Карточка 25

Алёна придумала 12 загадок, а Максим — в 2 раза меньше. Сколько загадок придумал Максим? Сколько всего загадок придумали оба мальчика?

Карточка 26

Мастер за день изготовил 24 детали, а его ученик — в 3 раза меньше. Сколько деталей изготовил ученик? Сколько всего деталей они изготовили вместе?

Карточка 28

На первом острове живёт 32 индейца, а на втором — в 4 раза меньше. Сколько индейцев живёт на втором острове? Сколько всего индейцев на двух островах?

Карточка 29

В куске было 54 метра ткани. Из этой ткани сшили 8 курток, расходуя по 3 метра на каждую. Сколько метров ткани осталось в куске?

В театре ученики первого класса заняли в партере 2 ряда по 9 мест и еще 13 мест в амфитеатре. Сколько всего мест заняли ученики первого класса?

Актовый зал освещает 6 люстр по 8 лампочек в каждой, да еще 7 лам­почек над сценой. Сколько всего лампочек освещает актовый зал?

К празднику купили 4 набора шариков по 10 штук в каждом наборе. Лопнули 12 шариков. Сколько шариков осталось на празднике?

В 3 одинаковых наборах 18 карандашей. Сколько карандашей будет в 7 таких наборах?

Начерти таблицу и реши задачу.

Для изготовления 5 одинаковых конструкторов потребовалось 35 деталей. Сколько деталей нужно для изготовления 8 таких конструкторов?

Начерти таблицу и реши задачу.

Крупу разложили на 6 одинаковых упаковок общей массой 12 кг. Сколько упаковок получится из 20 кг?

Начерти таблицу и реши задачу.

В 3 банки для засолки разложили 12 кг помидоров. Сколько банок потребуется для засолки 32 кг помидоров?

Начерти таблицу и реши задачу.

На 32р. купили 4 тетради. Сколько тетрадей можно купить на 56 рублей? на 16 рублей?

Начерти таблицу и реши задачу.

В 2 ведра помещается 16 кг картофеля. Сколько вёдер нужно, чтобы разложить 24 кг картофеля?

Начерти таблицу и реши задачу.

В 4 наборах 32 листа цветной бумаги. Сколько наборов составляют 72 листа бумаги?

Начерти таблицу и реши задачу.

• Начерти прямоугольник со сторонами 8 см и 4 см. Найди его площадь и периметр.
• Сравни:

12 смc1см2мм	7 мc74 дм	9 ммc1 см
14 смc1дм4см	8см7ммc90 мм	100 смc1 м

• Начерти прямоугольник со сторонами 5 см и 4 см. Найди его площадь и периметр.
• Сравни:

14 смc1см4мм	9 мc94 дм	9 ммc1 см
18 смc1дм8см	6см7ммc70 мм	10 смc1 дм

Расставь знаки «+», «-», «·», «: » так, чтобы равенства стали верными.

26*6*7=13	2*2*4=0
7*9*2=18	8*9*2=70
9*9*2=20	8*4*2=30
9*2*2=16	40*5*7=56

Из 12 м ткани портной сшил 6 одинаковых костюмов. Сколько метров ткани потребуется на 10 таких костюмов? на 7 костюмов?

Начерти таблицу и реши задачу.

В огороде собрали 24 кг моркови, редиса — в 4 раза меньше, чем моркови, а чеснока — в 5 раз больше, чем редиса. Сколько килограммов чеснока собрали?

Из 15 м тюля сшили 5 одинаковых занавесок. Сколько таких занавесок можно сшить из 21 м тюля? Сколько понадобится тюля, чтобы сшить 9 таких занавесок?

Начерти таблицу и реши задачу.

Формула Виета

Если в школьной геометрии чаще всего используется теорема Пифагора, то в школьной алгебре ведущую роль занимают формулы Виета. Теорема звучит так: 

Теорема Виета Сумма корней x2 + bx + c = 0 равна второму коэффициенту с противоположным знаком, а произведение корней равняется свободному члену.

Если дано x2 + bx + c = 0, где x₁ и x₂ являются корнями, то справедливы два равенства:

Знак системы, который принято обозначать фигурной скобкой, означает, что значения x₁ и x₂ удовлетворяют обоим равенствам.

Рассмотрим теорему Виета на примере: x2 + 4x + 3 = 0.

Пока неизвестно, какие корни имеет данное уравнение. Но в соответствии с теоремой можно записать, что сумма этих корней равна второму коэффициенту с противоположным знаком. Он равен четырем, значит будем использовать минус четыре:

Произведение корней по теореме соответствует свободному члену. В данном случае свободным членом является число три. Значит:

Необходимо проверить равна ли сумма корней −4, а произведение 3. Для этого найдем корни уравнения x2 + 4x + 3 = 0. Воспользуемся формулами для чётного второго коэффициента:

Получилось, что корнями уравнения являются числа −1 и −3. Их сумма равняется второму коэффициенту с противоположным знаком, а значит решение верное.

Произведение корней −1 и −3 по теореме Виета должно равняться свободному члену, то есть числу 3. Это условие также выполняется:

Результат проделанных вычислений в том, что мы убедились в справедливости выражения:

Когда дана сумма и произведение корней квадратного уравнения, принято начинать подбор подходящих корней. Теорема, обратная теореме Виета, при таких условиях может быть главным помощником. Вот она:

Обратная теорема Виета Если числа x1 и x2 таковы, что их сумма равна второму коэффициенту уравнения x2 + bx + c = 0, взятому с противоположным знаком, а их произведение равно свободному члену, то эти числа и есть корни x2 + bx + c = 0.

Обычно вся суть обратных теорем в том самом выводе, которое дает первая теорема. Так, при доказательстве теоремы Виета стало понятно, что сумма x₁ и x₂ равна −b, а их произведение равно c. В обратной теореме это и есть утверждение.

Пример 1. Решить при помощи теоремы Пифагора: x2 − 6x + 8 = 0.

Как решаем:

1. Для начала запишем сумму и произведение корней уравнения. Сумма будет равна 6, так как второй коэффициент равен −6. А произведение корней равно 8.
2. Когда у нас есть эти два равенства, можно подобрать подходящие корни, которые будут удовлетворять обоим равенствам системы.

   Чтобы проще подобрать корни, нужно их перемножить. Число 8 можно получить путем перемножения чисел 4 и 2 либо 1 и 8. Но значения x₁ и x₂ надо подбирать так, чтобы они удовлетворяли и второму равенству тоже.

   Можно сделать вывод, что значения 1 и 8 не подходят, так как они не удовлетворяют равенству x₁ + x₂ = 6. А значения 4 и 2 подходят обоим равенствам:

3. Значит числа 4 и 2 — корни уравнения x2 − 6x + 8 = 0. p>

Как разложить квадратное уравнение

С помощью теоремы Виета можно получить формулу разложения квадратного трехчлена на множители. Выглядит она так:

Формула разложения квадратного трехчлена Если x1 и x2 — корни квадратного трехчлена ax2 + bx + c, то справедливо равенство ax2 + bx + c = a (x − x1) (x − x2).

Понятие уравнения

Понятие уравнения обычно проходят в самом начале школьного курса алгебры. Его определяют, как равенство с неизвестным числом, которое нужно найти.

В школьной программе за 7 класс впервые появляется понятие переменных. Их принято обозначать латинскими буквами, которые принимают разные значения. Исходя из этого можно дать более полное определение уравнению.

Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.

Например, возьмем выражение 2 + 4 = 6. При вычислении левой части получается верное числовое равенство, то есть 6 = 6.

Уравнением можно назвать выражение 2 + x = 6, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.

Корень уравнения — то самое число, которое при подстановке на место неизвестной уравнивает выражения справа и слева.

Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.

Решить уравнение значит найти все возможные корни или убедиться, что их нет.

Решить уравнение с двумя, тремя и более переменными — это два, три и более значения переменных, которые обращают данное выражение в верное числовое равенство.