Как правильно объяснить ребёнку деление в столбик

Как делить в столбик четырехзначные, многозначные большие числа, многочлены на многочлены: примеры, объяснение

на доске решены примеры на деление столбиком трёх- и более значных чисел

В случае деления четырёхзначного числа на любое, которое содержит до 4 порядков одновременно, обратите внимание ребёнка на нюансы:

• определение правильного количества порядков после действия деления. Например, в примере 6734:56 должно получится двузначное целое число в графе «частное», а в примере 8956:1243 — однозначное целое,
• появление нулей в частном. Когда в ходе решения при переносе следующего числа делимого результат оказывается меньше делителя,
• проверку полученного результата посредством выполнения действия умножения. Этот нюанс актуален для деления больших чисел без остатка. Если последний присутствует, то советуйте ребёнку проверить себя и ещё раз разделить числа в столбик.

Ниже пример решения.

алгоритм деления столбиком четырёхзначного числа

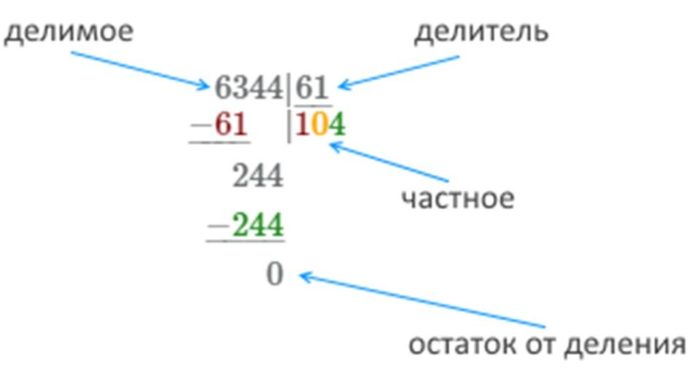
пример деления столбиком четырёхзначного числа на двузначное

Для больших многозначных чисел, которые делятся на конкретные значения меньше или равные им по количеству знаков, актуальны все алгоритмы, рассмотренные выше.

Ребёнку следует быть особенно внимательным в таких случаях и правильно определять:

• количество знаков у частного, то есть результата
• цифры у делимого для первого действия
• правильность переноса остальных чисел

Примеры подробного решения ниже.

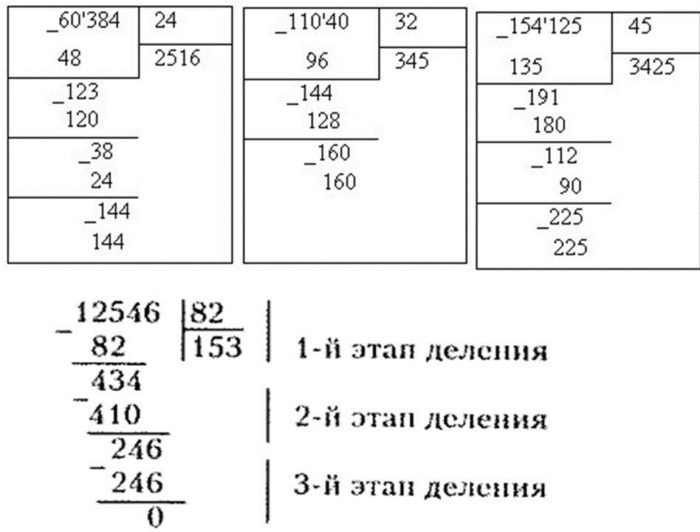
примеры деления столбиком многочленов

При совершении действия деления над многочленами обращайте внимание детей на ряд особенностей:

• у действия может быть остаток либо отсутствовать. В первом случае запишите его в числителе, а делитель в знаменателе,
• для совершения действия вычитания дописывайте в многочлен недостающие степени функции, умноженные на ноль,
• совершайте преобразование многочленов путём выделения повторяющихся дву-/многочленов. Тогда их сократите и получится результат без остатка.

Ниже ряд подробных примеров с решениями.

примеры деления многочленов в столбик

Примеры деления в столбик на двузначное число

Рассмотрим некоторые примеры. Они довольно простые и помогут понять основные моменты данного способа.

Найдём значение частного чисел 265 и 53:

Найдем результат деления чисел 624 и 52:

Рассмотрим более сложные случаи деления в столбик. Найдем значение частного чисел 1610 и 35:

Деление пятизначного числа на двузначное. Узнаем значение частного чисел 10150 и 35:

Пример 5

Деление многозначного числа на двузначное с остатком. Вычислим, чему будет равно частное чисел 1978 и 38:

Деление на двузначное число можно выполнять в столбик и устно, но многозначные числа устно считать намного сложнее. Немногие школьники могут похвастаться подобными умениями.

Освоение процесса деления поможет школьникам в дальнейшем обучении. Так же существует немало тренажеров и онлайн-калькуляторов, которые можно использовать в свою пользу.

Осваиваем операцию разделения (деления) на части в игровой форме

На этом этапе необходимо сформировать у ребёнка понимание того, что деление – это разделение чего-либо на равные части. Самый просто способ научить ребёнка этому – предложить ему разделить некоторое количество предметов между ним его друзьями или членами семьи.

Допустим, возьмите 8 одинаковых кубиков и предложите ребёнку разделить на две равные части – для него и другого человека. Варьируйте и усложняйте задание, предложите ребёнку разделить 8 кубиков не на двоих, а на четырёх человек. Проанализируйте вместе с ним результат. Меняйте составляющие, пробуйте с другим количеством предметов и людей, на которые нужно разделить эти предметы.

Важно: Следите, чтобы вначале ребёнок оперировал с чётным количеством предметов, для того, чтобы результатом деления было одинаковое количество частей. Это окажется полезным  на следующем этапе, когда ребёнку будет нужно понять, что деление – это операция обратная умножению

Решение задач на деление с остатком

Простые задачи легко решить, если составить модель-схему условия и решения задачи на числовом луче.

Рассмотрите пример задачи:

Повар испек 17 творожных и 19 брусничных ватрушек. На тарелки положит по три штуки одного сорта. Узнайте, сколько нужно тарелок и сколько ватрушек останется.

Решение:

Ответ: для творожных ватрушек нужно 5 тарелок, две останутся; для брусничных — 5 тарелок, одна ватрушка останется.

Составьте задачу на деление с остатком, выбрав подходящее выражение:

Проверьте рассуждение. Для задачи подойдет второе выражение, а первое и последнее – не подходят, потому что это табличные случаи.

Пример задачи: На пальто пришивается 4 пуговицы. На сколько таких пальто хватит 15 пуговиц? Сколько пуговиц останется?

Ответ: пуговиц хватит на три пальто. Останется 3 пуговицы.

Придумайте задачу к схеме:

Мама купила 21 конфету и поделила по 8 штук детям. Сколько детей в семье и сколько конфет мама оставила себе?

Решение:

21 : 8 = 2 (ост.5)

Ответ: в семье двое детей. Мама оставила 5 конфет.

Умения решать задачи по математике помогают в жизни.

Подсказка: решить задачу можно округлив величины. 90 – это девять десятков, а 28 округлим до трех десятков.

Проверьте:

Ответ: Незнайка купит 3 стаканчика с мороженным. У него останется 6 рублей.

Как научиться делить в столбик с остатком

Деление с остатком – следующий этап обучения. Во время таких действий делимое невозможно ровно разделить на части. Ответ примера будет иметь неделимый кусок, меньший делителя. Чтобы школьник быстрее понял смысл математических действий, тему объясняют на доступных примерах.
На подносе находится 34 конфеты, которые нужно разделить на 8 детей. Когда каждый ребенок получит по 4 конфеты, на столе останется еще 2 штуки. Это и будет остаток. Вычисления выглядят следующим образом:
34 : 8= 4 ост (2). Откуда взялась цифра «2»? 8 х 4= 32, 34 — 32= 2.
Принцип деления уголком с остатком аналогичен классическому, с одной разницей – наличием остатка.

Для примера разделим 235 на 14.

235 — делимое, расположим слева, делитель (14) напишем правее. Оба значения между собой разделим уголком. Приступим к поиску целого. 23>14, в данном числе помещается 1 делитель. Единицу запишем внизу под уголком. 23 — 14 = 9.

Во время решения примеров с остатком, ответ может быть записан двумя способами:

• в виде дроби, когда в числителе размещают остаток, а в знаменатель записывают делитель:11/16,
• но чаще всего ответ записывают словами: 6 целых и 11 в остатке.

Методика деления в столбик

Существует определенный алгоритм для деления в столбик. Изучается он в начальных классах средних образовательных школ. Методику можно применять не только для положительных, но и отрицательных значений. При этом нужно учитывать знак:

1. Деление отрицательной величины на отрицательную — положительное значение.
2. При делении положительного на отрицательное или наоборот — отрицательная величина.

Алгоритм без остатка

Методика применяется в том случае, когда делимое является не простым числом, а содержит множители. Кроме того, при его делении на делитель, не соответствующий одному из признаков деления. Например, 33 делится на 2 с остатком. Однако, когда делитель равен 3, то последнего нет.

Для применения алгоритма нужно наглядно разобрать следующий пример: требуется разделить 78 на 2. Методика выполнения этой операции имеет следующий вид:

1. Записать делимое с левой стороны, а делитель — справа.
2. По карточке простых чисел или при помощи ручного метода необходимо определить принадлежность делимого к простым значениям (78 делится на 2, поскольку заканчивается на четную цифру 8).
3. Разделить две значения вертикальной чертой.
4. Выделить I неполное делимое: 7.
5. По таблице умножения подобрать ближайшее целое (3). При произведении его на делитель должно получиться значение, которое меньше первого неполного делимого (3 * 2 = 6 < 7). Если записать 4, то 4 * 2 = 8 > 7 (вариант не подходит).
6. Записать число, полученное при умножении делителя на подобранное значение, под I неполным делимым. Произвести операцию вычитания (7 — 6 = 1).
7. Результат вычитания (1), который называется остатком, не делится на 2. Следовательно, нужно дописать II неполное делимое (18). Если по какой-то причине, результат делится на делитель, то подобранное значение является неверным.
8. Значение 18 делится на 2, т. е. 18/2 = 9.
9. Результат деления 78 на 2 равен 39.

Операция с остатком

Не во всех случаях результат деления двух чисел является целой величиной. В школьной программе встречается группа примеров, в которых требуется найти остаток, полученный при выполнении операции деления 2 значений (77/3). Алгоритм похож на предыдущий, но имеются некоторые особенности:

1. Два числа записываются, как и в предыдущем случае.
2. Принадлежность к множеству простых чисел не проверяется.
3. Выделить I неполное делимое: 7.
4. Подобрать ближайшее целое число, записав его в результат: 2.
5. Выполнить проверку: 3 * 2 = 6 < 7 (значение подходит).
6. Записать 6 под 7, а затем выполнить операцию вычитания: 7 — 6 = 1. Остаток меньше 3, следовательно, число подобрано правильно.
7. Выполнить подбор множителя для 17: целочисленного значения нет. Следовательно, нужно подобрать ближайшее целое: 5.
8. Произвести проверку: 3 * 5 = 15 < 17.
9. Записать 5 в результат и определить остаток: 17 — 15 = 2.
10. Результат деления 77 на 3 эквивалентен: 25 с остатком 2.

Таким образом, для выполнения операции деления двузначного числа на однозначное нужно знать признаки делимости величин, а также основные алгоритмы деления с остатком и без него.

Деление с остатком

К этим вычислениям нужно приступать только тогда, когда предыдущий материал выучен безупречно, алгоритм решения детально разобран и действия выполняются за считанные минуты. Как только ребенок детально разобрался в вопросе, можно двигаться дальше.

Особенность деления с остатком в том, что нужно выделить основную часть и понять, какое же число останется в итоге. На начальных порах у школьника может возникнуть барьер, ведь до этого все примеры решались легко, а теперь нужен иной подход к вычислениям.

Но опять-таки решение основывается на знании таблицы умножения и умении разделить большое число на несколько составляющих.

Пример: 

83:9, ребенок знает, что 81:9=9. 83-81=2. Значит, ответ: 9 и 2 в остатке.

114:5, 100:5=20, 10:5=2, 4 на 5 разделить невозможно. Соответственно, 114:5=100:5+20:5 и 4 = 22 и 4 в остатке.

Можно изучать этот тип примеров с помощью денежных операций, ведь сдача, полученная после оплаты покупок, — это как раз и есть остаток. Или же использовать для этой цели еду либо игрушки: куски торта, куклы можно делить на всех участников игрового процесса, подобрав такое количество, чтобы обязательно оставался «лишний» кусочек.

Разложение на слагаемые

Интересным вариантом алгоритма является метод разложения числа на слагаемые. Его суть очень проста: представление делимого в виде суммы нескольких слагаемых, при условии деления каждого из них на выбранное число. Инструкция является очень простой. Она может стать дополнительным математическим тренажером для ребенка, поскольку развивает мышление и улучшает память. Для деления любого числа на другое нужно строго выполнить следующие шаги:

1. Методом подбора разложить число на слагаемые, каждое из которых должно делиться на делитель.
2. Разделить значения в первом пункте на заданный делитель.
3. Сложить результаты для получения итоговой суммы.

На первом шаге специалисты рекомендуют слагаемые отделить от делителя круглыми скобками. Записывать нужно в одну строчку для наглядности. Далее следует выполнить деление или сократить слагаемые на множитель. Полученную сумму сложить и записать ответ. Например, следует вычислить 156/4.

Выполняется эта процедура таким образом:

1. Разложение: 156 = (140 + 16) = (160 — 4).
2. Деление: (140 + 16) / 4.
3. Результат: 35 + 4 = 39.

Специалисты рекомендуют представлять число в удобной форме, а не только в виде суммы. Доказывать, что это значение является простым не нужно, поскольку не стоит такая задача. Этот алгоритм необходимо записать на картонную карточку. Чтобы научиться по нему решать, можно также написать текст или инструкцию. Одним словом, следует руководствоваться удобством для ребенка.

От простого к сложному

Дети обычно проходят тему деления в столбик, когда переходят в 3 или 4 класс. На момент обучения ими в обязательном порядке должны быть усвоены простые навыки сложения и вычитания, а принципы умножения и деления должны быть известны в теории и достаточно хорошо на практике. Запомнить правила деления столбиком сложно, если до сих пор не выучена таблица умножения.

И так, что такое деление? Это разделение определенного количества на равные части. Ребенку стоит объяснить это на примере. Например, возьмите 12 яблок и предложите каждому члену семьи (маме, папе, брату/сестре и самому ученику) раздать яблоки поровну. Затем усложните задачу и предложить раздать 12 яблок трем членам семьи. Оговорите полученный в обоих случаях результат со своим малышом. Старайтесь сразу донести суть, заключающуюся в обратности умножения и деления, на разных примерах таблицы.

Скажите ребенку, что из двух чисел, участвующих в умножении (например, 4х5=20), при делении ответом будет второе из них (20/4=5 или 20/5=4).

Деление на двузначное число с остатком

При делении на двузначное число с остатком рассуждать нужно так же.

1. Найдем частное.

В частном будет одна цифра. Чтобы легче было найти цифру частного, разделим 299 не на 34, а на 30.

9 – это пробная цифра частного, ее нельзя сразу записывать в частном, а нужно сначала проверить, подойдет ли она. Умножим 34 на 9.

306 больше, чем делимое 299. Значит, цифра 9 не подходит. Проверим цифру 8.

Значит, цифра 8 подойдет. Остаток меньше, чем делитель. Записываем в частном цифру 8.

Значение частного чисел 299 и 34 – 8 и остаток 27.

2. Рассмотрим еще один случай деления.

В частном будет одна цифра. Чтобы легче было найти цифру частного, разделим 191 не на 46, а на 40.

4 – это только пробная цифра, ее нельзя сразу записывать в частном, а нужно сначала проверить, подойдет ли она. Умножим 46 на 4.

Остаток 7 меньше, чем делитель 46. Значит, цифра частого 4 подходит, запишем ее.

Значение частного чисел 191 и 46 – 4 и остаток 7.

Деление на двузначное число без остатка

Рассмотрим сначала, как выполнить деление на двузначное число без остатка.

В значении частного будет одна цифра. Чтобы легче было подобрать цифру частного, разделим 312 не на 52, а на 50:

6 – это пробная цифра, ее нельзя сразу записывать в частном, ведь мы делим не на 50, а на 52. Сначала нужно проверить, подойдет ли цифра 6. Умножим 52 на 6.

Цифра подошла. Значение частного будет 6.

Рассмотрим еще один случай деления.

В значении частного будет одна цифра. Чтобы легче было подобрать цифру частного, разделим 469 не на 67, а на 60.

7 – это пробная цифра, ее нельзя сразу записывать в частном, ведь мы 469 делим не на 60, а на 67. Сначала нужно проверить, подойдет ли цифра 7. Умножим 67 на 7.

Мы видим, что цифра 7 подходит. Значит, значение частного будет 7.

Деление в столбик – правила

Для того, чтобы уметь делить в столбик необходимо знать некоторые правила. Именно об этом и пойдет далее речь. Ведь деление в столбик невозможно освоить если не знать элементарного – таблицы умножения. Считать простые примеры на умножение необходимо быстро и в уме. Это только в начале обычно дети пользуются черновиками, чтобы подобрать множитель, таким образом найти частное. Еще надобно уметь разбивать числа на сотни, десятки, тысячи – не путаться и в этих понятиях. Для наглядности, где делимое, где делитель, где частное можете изучить термины на изображении ниже.

Что нужно знать для деления в столбик?

Прежде, чем приступать к делению, следует проверить ребенка на знания элементарных правил. Ведь пропускать математику нельзя. А если пропуски все же были, то нужно изучить тот материал, что изучали ранее на уроках в школе

Понадобится обратить внимание на такие знания, как:

Запомнил ли школьник, как называются все элементы, участвующие в процессе деления.

Обратите внимание на знание таблицы умножения ребенком.
Еще ребенок должен усвоить, какие бывают разряды числа (единицы, десятки, сотни).

Пример: 

1. 57: 3, где 57 – это делимое, число, что разделяют на доли, а 3 – это делитель, указывающий, на сколько делить предыдущее число.
2. Определяемся, вначале какие единицы выделить в делимом для осуществления деления в столбик числа 57. Число 5 > 3.
3. Узнайте, сколько раз следует взять число 3, чтобы получить 5. Результат 3 · 1 = 3 ≤ 5. Значит подходит и 1 поставьте в качестве первой цифры частного.
4. Теперь вычитание: 5 — 3 = 2. Остаток 2 и единицу сносим, выходит 27.
5. Находим теперь, на какое число нужно умножить 3, чтобы результат был 27. Согласно таблице умножения 3 · 9 = 27.
6. Итого результат 19.

Умножение, деление – взаимосвязаны между собой, хотя и противоположные операции. Чтобы проверить, верно ли нашли частное, необходимо выполнить умножение. Потому таблица умножения и умение умножать на черновике без калькулятора всегда пригодится ребенку, также еще при умножении следует уметь правильно прибавлять, а при делении в столбик вычитать. В математики все действия с числами между собой взаимосвязаны.

Ниже смотрите пример деления в столбик 536 на 4. Действия с трехзначным делимым выполняются аналогично, что и с двухзначным.

Деление

Деление в школе начинают учить уже с третьего класса. Школьники только изучают азы процесса, выполняют самые простые примеры на это действие.

Примеры подобны умножению, только детей учат таблице деления, а не умножения. Школьники должны уловить саму суть, что означает поделить число на несколько частей, изучают, что такое делимое, делитель, частное. Узнают, как проверить умножением правильность решения примера или же задачи. В столбик дети еще не считают, так как даются самые простые примеры и все числа из таблицы умножения. Пример: 81 : 9 = 9.

Процесс деления в четвертом классе значительно усложняется. Детям дают вначале года вспомнить, что они учили в третьем классе, а далее уже начинают осваивать технику деления чисел в столбик. Именно за этот учебный год осваивают такие знания. Ниже приведен алгоритм решения примеров в столбик с подробным описанием процесса.

Здесь даже учтено то, что возможно будет остаток при делении, что число получится не цельным, а через запятую.

Деление двузначного числа на однозначное

Ребята, вы меня узнали? Люблю наряжаться на маскарад. Вот прицепил такие усы, думал, что буду похож на фокусника. Чудеса начинаются.

Такие задания называют примерами с «усиками». Да, да, но усики носят не люди, кто делит, а сами примеры. Рисовать их нужно простым карандашом, а когда научитесь быстро считать, то просто представляйте в голове.

Устное деление двузначного на однозначное

Задание 1.

Пусть надо решить, сколько будет

К «усикам» запишем такие два слагаемых, которые делятся на 8, а в сумме дают 96.

Самое главное — это не ошибиться в подборе первого «усика». Надо запомнить, что он всегда больше, чем второй. Ищем его, умножая 8 на 10. Если не подойдет, то будем умножать на 20, на 30. Главное, чтобы было круглое число.

Все понятно? Будем тренироваться.

Задание 2.

Задание 3.

Попробуем разделить 90 на два. «Первый усик» явно не 20, тогда второй будет 70. Знаем, что «второй усик» не может быть больше первого.

Вижу, что не 60, потому что 30 разделить на два — это не табличный случай.

Следовательно, 2 ∙ 40 = 80. Значит «первый усик» предположительно 80. «Второй усик» тогда найдем вычитанием: 90 – 80 = 10. Десять разделить на два, это таблица.

Как думаете, вы справитесь с делением? Когда встречаете случаи, где двузначное число делится на однозначное, и примеры не относятся к таблице умножения, то решайте подбором «усиков». Разбивайте делимое на подходящие слагаемые. Их можно записать суммой в скобочках, а при делении использовать правило деления суммы на число.

Решите задачу.

Таня выполнила 96 примеров, а Коля в 4 раза меньше. Сколько примеров решил Коля?

Чтобы ответить на вопрос задачи, надо выполнить действие деления.

96 : 4 =

«Усиками» будут 80 и 16, получается сумма 80 + 16. Значит, каждое из этих слагаемых разделите на 4, а частные сложите.

Ответ: 24

Деление столбиком двузначное на однозначное

Письменное деление уголком просто невозможно усвоить без блестящего знания таблицы умножения. Это просто трата времени и нервов. В древности в римских школах ее заучивали хором на распев. Знаете ответы на «отлично», тогда переходите на примеры деления в столбик.

Задание 1.

Пусть надо 84 разделить на три. Посмотрите на запись. Такой значок означает деление уголком. Уголок имеет наверху делитель, на который делим. Под чертой — результат, который ищем. Он называется частным.

Нам надо узнать, чему равно частное. Но прежде определим, сколько цифр будет в результате. Это очень важный шаг, поэтому упускать его нельзя. Как мы будем это делать? Посмотрите на первую цифру. Это восьмерка. Восемь больше трех. Значит, она может дать нам полноценную цифру в частном. Ставим точку. После восьмерки еще одна цифра, это значит, что частное — двузначное число. Под чертой в уголке карандашом поставьте вторую точку.

Первое неполное делимое — восьмерка. Начинаем ее делить на три, ищем табличный случай. Легче всего уменьшать 8 на единицу.

8 – 1 = 7. В таблице нет деления семи на три.

Уменьшаем еще на 1.

7 – 1 = 6. Шесть делится на три, получается — по два. Записываем 2 в частное под чертой.

Теперь мы должны понять, сколько не разделили. Ведь разделили всего шесть.

А надо было разделить восемь.

Два осталось неразделенным. Это остаток. Он должен быть меньше делителя.

Давайте проверим: два меньше трех.

Да, действительно. Мы сделали все правильно. Этот шаг очень важен. Не забывайте сравнивать остаток с делителем.

После этого сносим следующую цифру с тем, чтобы получить новое неполное делимое

Обратите внимание: нужно писать каждую цифру в своей клетке. Получается неполное делимое 24

Ответ: 28.

Задание 2.

Решите пример столбиком 96 : 4 =

Проверьте:

Ура! Наш математический маршрут пройден. Знания-сокровища из цветных лент превратились в волшебную радугу. Что же у нас вышло, что мы унесем в нашем сундуке. Закончите предложения:

Деление на двузначное число

Когда ученик 3-го класса усвоил деление на однозначное число, можно приступать к следующему этапу — работе с двузначными цифрами. Начинайте с простых, явных примеров, чтобы малыш понял алгоритм действий при делении на двузначные числа. Например, возьмите числа 196 и 28 и объясните принцип:

1. Сначала подберите примерное число для ответа. Для этого выясните приблизительно, сколько цифр 28 поместится в 196. Для удобства можно округлять оба числа: 200:30. Получится не больше 6. Полученное число не нужно записывать, это только догадка.

2. Проверяем результат умножением: 28х6. Получается 196. Предположения оказались верными.

3. Запишите ответ: 196:28 =6.

Еще один вариант обучения: деление на двузначное число уголком. Такой способ больше подходит для работы с числами от четырех разрядов, то есть тысяч. Приведем простой пример:

Напишите на листе бумаги 4070, начертите уголок и подпишите делитель — 74.
Определите, с какого числа начнете делить. Спросите у ребенка, можно ли разделить 4 на 74, 40? В результате малыш поймет, что сначала нужно ограничиться числом 407. Очертите полученную цифру сверху полукругом. 0 останется в стороне.
Теперь нужно выяснить, сколько 74 поместится в 407. Действуем с помощью логики и проверки умножением. Получится 5. Записываем результат под уголком (под делителем).
Теперь умножаем 74 на 5 и записываем результат под делимым. Получится 370

Важно начинать запись с первого числа слева.
После записи нужно подвести горизонтальную черту и отнять 370 от 407. Получится 37.
37 разделить на 74 нельзя, поэтому вниз сносится оставшийся в верхнем ряду 0.
Теперь делим 370 на 74

Подбираем множитель (5) и записываем его под уголком.
Умножаем 5 на 74, записываем результат в столбик. Получится 370.
Опять получаем разность. Результат будет равен 0. Значит, деление считается завершенным без остатка.

4070:74=55. Частное смотрим под уголком.

Для проверки правильности решение произведите умножение: 74х55=4070.

Алгоритм деления в столбик

Для этого алгоритма следует воспользоваться наглядным примером (рис. 1). Следует разделить 792 на 2. Первоначальное число является трехзначным и состоит единиц, десятков и сотен. Записывается операция в столбик, как показано на рисунке 1. Цифра «7» — первое неполное делимое. Вторым неполным называется делимое, полученное на втором цикле операции, а третьим — на третьем.

Рисунок 1. Графическое представление деления трехзначного числа в столбик.

Исходя из рисунка 1, можно составить алгоритм деления в столбик. Его можно применять не только для трехзначного, но и шестизначного, десятизначного и многозначного чисел. Единственное правило: количество цифр делимого должно быть больше, чем число знаков делителя. Алгоритм имеет такой вид:

1. Записать делимое и делитель.
2. Выделить первое неполное делимое (7): подобрать целое число (должно быть не больше I делимого), на которое следует умножить делитель для получения приблизительного значения первого (3, поскольку 3 * 2 = 6. Если взять 4, то 8 > 7).
3. Произвести умножение и вычесть со значения первого (7 — 6 = 1), записав остаток. Если последнего нет, то ничего переносить не нужно.
4. Взять II неполное делимое с учетом остатка (19).
5. Подобрать множитель: 2 * 9 = 18 < 19.
6. Произвести операцию вычитания с выделением остатка: 19 — 18 = 1.
7. С учетом остатка (1) взять III неполное делимое (2).
8. Подобрать множитель: 2 * 6 = 12.
9. В остатке 0. Следовательно, операция закончена.

Деление в столбик с остатком осуществляется по такому же алгоритму. Например, 793 на два делится только с остатком. Чтобы не повторять вычисления с самого начала, можно воспользоваться уже готовыми. Для этого необходимо вернуться в седьмой пункт предыдущего алгоритма:

1. Остаток (1) и III неполное делимое (3): 13.
2. Множитель равен 6: 2 * 6 = 12 < 13.
3. Остаток эквивалентен 1, но всего III неполных делителя. Операция выполнена с остатком 1.

Как объяснить деление с остатком?

Иногда разделить на равные доли невозможно. Легче всего объяснить такую ситуацию школьнику на несложной задаче. Например:

Решение столбиком с остатком, по математическому правилу, записывается точно так же, как и без него. Разница лишь в том, что в конце остаток будет. В этом варианте правильно прописать количество целых единиц и количество единиц в остатке (пример: 4 целых и 9 в остатке).

Обучение школьника должно проходить поэтапно, от простых примеров к более сложным.  Если нет понимания простых действий в делении, значит, нужно повторить информацию еще раз. Постепенно решение примеров начнет происходить быстрее и увереннее. Главное – поверить в силы маленького человека, быть терпеливым, и тогда делить числа методом столбца станет интересным занятием для школьника.

Скачать карточки

В качестве домашнего математического тренажера используйте карточки с примерами. В них включайте разные случаи: с однозначными и многозначными числами, с нулями, деление с полным результатом и остатком. Скачать карточки можно бесплатно. Раздаточный материал обязательно следует напечатать для проверочной работы.

Ошибки с делением у детей в начальной школе встречаются довольно часто. Уделите этой теме максимум внимания и времени, чтобы усвоение последующего материала проходило без запинок. Используйте карточки, видеоуроки, постоянную тренировку навыка и повторение пройденных тем и правил в игровой форме. Тогда домашние уроки не навеют на ребенку скуку и пройдут с максимальной пользой.

Понравился наш контент? Подпишитесь на канал в .

Правила записи при делении столбиком

Начнем с изучения правил записи делимого, делителя, всех промежуточных выкладок и результатов при делении натуральных чисел столбиком. Сразу скажем, что письменно выполнять деление столбиком удобнее всего на бумаге с клетчатой разлиновкой – так меньше шансов сбиться с нужной строки и столбца.

Сначала в одной строке слева направо записываются делимое и делитель, после чего между записанными числами изображается символ вида . Например, если делимым является число 6 105, а делителем – 55, то их правильная запись при делении в столбик будет такой:

Посмотрите на следующую схему, иллюстрирующую места для записи делимого, делителя, частного, остатка и промежуточных вычислений при делении столбиком.

Из приведенной схемы видно, что искомое частное (или неполное частное при делении с остатком) будет записано ниже делителя под горизонтальной чертой. А промежуточные вычисления будут вестись ниже делимого, и нужно заранее позаботиться о наличии места на странице. При этом следует руководствоваться правилом: чем больше разница в количестве знаков в записях делимого и делителя, тем больше потребуется места. Например, при делении столбиком натурального числа 614 808 на 51 234 (614 808 – шестизначное число, 51 234 – пятизначное число, разница в количестве знаков в записях равна 6−5=1) для промежуточных вычислений потребуется меньше места, чем при делении чисел 8 058 и 4 (здесь разница в количестве знаков равна 4−1=3). Для подтверждения своих слов приводим законченные записи деления столбиком этих натуральных чисел:

Теперь можно переходить непосредственно к процессу деления натуральных чисел столбиком.

Разбор примеров на деление столбиком на двузначное число

Сначала рассмотрим простые случаи деления, когда в частном получается однозначное число.

Первое неполное делимое 265. Больше в делимом цифр нет. Значит в частном будет однозначное число.

Чтобы было легче подобрать цифру частного, разделим 265 не на 53, а на близкое круглое число 50. Для этого 265 разделим на 10, будет 26 (остаток 5). И 26 разделим на 5, будет 5 (остаток 1). Цифру 5 нельзя сразу записывать в частном, поскольку это пробная цифра. Сначала нужно проверить, подойдет ли она. Умножим 53*5=265. Мы видим, что цифра 5 подошла. И теперь можем ее записать в частном под уголок. 265-265=0. Деление выполнено без остатка.

Значение частного чисел 265 и 53 равно 5.

Иногда при делении пробная цифра частного не подходит, и тогда ее нужно менять.

В частном будет однозначное число. 

Чтобы было легче подобрать цифру частного, разделим 184 не на 23, а на 20. Для этого разделим 184 на 10, будет 18 (остаток 4). И 18 разделим на 2, будет 9. 9 – это пробная цифра, мы ее сразу писать в частном не будем, а проверим, подойдет ли она. Умножим 23*9=207. 207 больше, чем 184. Мы видим, что цифра 9 не подходит. В частном будет меньше 9. Попробуем, подойдет ли цифра 8. Умножим 23*8=184. Мы видим, что цифра 8 подходит. Можем ее записать в частном. 184-184=0. Деление выполнено без остатка.

Значение частного чисел 184 и 23 равно 8.

Рассмотрим более сложные случаи деления.

Первое неполное делимое – 76 десятков. Значит, в частном будут 2 цифры.

Определим первую цифру частного. Разделим 76 на 24. Чтобы легче было подобрать цифру частного, разделим 76 не на 24, а на 20. То есть нужно 76 разделить на 10, будет 7 (остаток 6). И 7 разделим на 2, получится 3 (остаток 1). 3 – это пробная цифра частного. Сначала проверим, подойдет ли она. Умножим 24*3=72 . 76-72=4. Остаток меньше делителя. Значит, цифра 3 подошла и теперь мы ее можем записать на месте десятков частного. 72 пишем под первым неполным делимым, между ними ставим знак минус, под чертой записываем остаток.

Продолжим деление. Перепишем в строку с остатком цифру 8, следующую за первым неполным делимым. Получим следующее неполное делимое – 48 единиц. Разделим 48 на 24. Чтобы было легче подобрать цифру частного, разделим 48 не на 24, а на 20. То есть разделим 48 на 10, будет 4 (остаток 8). И 4 разделим на 2, будет 2. Это пробная цифра частного. Мы должны сначала проверить, подойдет ли она. Умножим 24*2=48. Мы видим, что цифра 2 подошла и, значит, можем ее записать на месте единиц частного. 48-48=0, деление выполнено без остатка.

 Значение частного чисел 768 и 24 равно 32.

Первое неполное делимое – 153 сотни, значит, в частном будут три цифры.

Определим первую цифру частного. Разделим 153 на 56. Чтобы легче было подобрать цифру частного, разделим 153 не на 56, а на 50. Для этого разделим 153 на 10, будет 15 (остаток 3). И 15 разделим на 5, будет 3. 3 – это пробная цифра частного. Помните: ее нельзя сразу записывать в частном, а нужно сначала проверить, подойдет ли она. Умножим 56*3=168. 168 больше, чем 153. Значит, в частном будет меньше, чем 3. Проверим, подойдет ли цифра 2. Умножим 56*2=112. 153-112=41. Остаток меньше делителя, значит, цифра 2 подходит, ее можно записать на месте сотен в частном.

Образуем следующее неполное делимое. 153-112=41. Переписываем в ту же строку цифру 4, следующую за первым неполным делимым. Получаем второе неполное делимое  414 десятков. Разделим 414 на 56. Чтобы удобнее было подобрать цифру частного, разделим 414 не на 56, а на 50. 414:10=41(ост.4). 41:5=8(ост.1). Помните: 8 – это пробная цифра. Проверим ее. 56*8=448. 448 больше, чем 414, значит, в частном будет меньше, чем 8. Проверим, подойдет ли цифра 7. Умножим 56 на 7, получится 392. 414-392=22. Остаток меньше делителя. Значит, цифра подошла и в частном на месте десятков можем записать 7.

Пишем в строку с новым остатком 4 единицы. Значит следующее неполное делимое – 224 единицы. Продолжим деление. Разделим 224 на 56. Чтобы легче было подобрать цифру частного, разделим 224 на 50. То есть сначала на 10, будет 22 (остаток 4). И 22 разделим на 5, будет 4 (остаток 2). 4 – это пробная цифра, проверим ее, подойдет ли она. 56*4=224. И мы видим, что цифра подошла. Запишем 4 на месте единиц в частном. 224-224=0, деление выполнено без остатка.

Значение частного чисел 15344 и 56 равно 274.