Деление натуральных чисел столбиком: правило, примеры

Делим в столбик

Этот метод используют, когда выполнить действие устно нельзя. Здесь ответ дети подбирают. Если ребенок хорошо знает умножение и вычитание, то решение этих примеров доставит большое удовольствие.

Родители акцентируют внимание на то, что обычный знак деления заменяется двумя чертами, которые похожи на перевернутую букву >. Слева стоит делимое, справа над чертой – делитель, а под чертой – частное

Делимое состоит из двух разрядов: десятки и единицы. Начинаем выполнять действие с крайней цифры слева. Взрослые напоминают школьнику, что есть деление с остатком. Оно пригодится в этом случае.

9 : 7

Задаем наш традиционный вопрос: какое надо подобрать число, чтобы при умножении его на 7, получился ответ, близкий к 9. Это 1. Ее пишем в частное (под чертой).

Проверяем.

7?1 = 7

Ставим под 9 и вычитаем. Знак равенства заменяется в таких примерах горизонтальной чертой. Это надо проговаривать ребенку.

9 — 7 = 2

К остатку сносим 8 из делимого. Полученное число (28) делим на 7 Ответ: 4. Пишем рядом с единицей в частном.

Проверяем: 4 ?7 =28

Полученный результат вычитаем из 28. Остаток 0. Задание выполнено.

Просмотры 152

Поделитесь записью в соцсетях

Деление с остатком целых положительных чисел

Деление — это разбиение целого на равные части.

Остаток от деления — это число, которое образуется при делении с остатком. То есть то, что «влезло» и осталось, как хвостик.

Чтобы научиться делить числа с остатком, нужно усвоить некоторые правила. Начнем!

Все целые положительные числа являются натуральными. Поэтому деление целых чисел выполняется по всем правилам деления с остатком натуральных чисел.

Самый удобный способ деления — это столбик.

Попрактикуемся в решении.

Пример

Разделить 14671 на 54.

Как решаем:

Выполним деление столбиком:

Неполное частное равно 271, остаток — 37.

Ответ: 14671 : 54 = 271(остаток 37).

Представление делимого в виде произведения

При делении натуральных чисел не стоит забывать о свойстве деления произведения двух чисел на натуральное число. Иногда делимое можно представить в виде произведения, один из множителей в котором делится на делитель. 

Рассмотрим типичные случаи.

Пример 2. Представление делимого в виде произведения

Разделим 30 на 3.

Делимое 30 можно представить в виде произведения30=3·10.

Имеем: 30÷3=3·10÷3

Воспользовавшись свойством деления произведения двух чисел, получаем:

3·10÷3=3÷3·10=1·10=10

30÷3=10

Приведем еще несколько аналогичных примеров.

Пример 3. Представление делимого в виде произведения

Вычислим частное 7200÷72.

Представляем делимое в виде 7200=72·100. При этом, результат деления будет следующим:

7200÷72=72·100÷72=72÷72÷100=100

Пример 4. Представление делимого в виде произведения

Вычислим частное: 1600000÷160.

1600000=160·10000

1600000÷160=160·10000÷160=160÷160·10000=10000

В более сложных примерах удобно пользоваться таблицей умножения. Проиллюстрируем это.

Пример 5. Представление делимого в виде произведения

Разделим 5400 на 9.

Таблица умножения подсказывает нам, что 54 делится на 9, поэтому делимое целесообразно представить в виде произведения:

5400=54·100.

Теперь закончим деление:

5400÷9=54·100÷9=54÷9·100=6·100=600

Для закрепления данного материала рассмотрим еще один пример, уже без подробных словесных пояснений.

Пример 6. Представление делимого в виде произведения

Посчитаем, сколько будет 120 разделить на 4.

120=12·10

120÷4=12·10÷4=12÷4·10=3·10=30

Как разделить столбиком одну десятичную дробь на другую

Все просто: умножаем делимое и делитель на 10, 100 и так далее — так, чтобы делитель превратился в натуральное число. А потом решаем также, как в примере выше: 

1. Переносим запятую в делимом и делителе вправо на то количество знаков, которое необходимо для превращения делителя в натуральное число. Если в делимом не хватит знаков, дописываем в него нули с правой стороны.

2. После этого делим дробь столбиком на получившееся натуральное число.

Пример: поделить столбиком 63,42 на 2,1

Как решаем Переносим запятую на один знак вправо, чтобы делитель (2,1) стало натуральным числом. Запятую переносим в обоих числах — у нас получается 634,2÷21. Затем производим деление

Ответ: 63,42÷2,1 = 30,2

Дроби

Эта тема обычно является одной из самых сложных. А все потому, что школьникам сложно понять, почему 1 можно представить как 33 или 55. И хоть в школьной программе этому уделяется немало часов, многие ученики все-таки испытывают трудности. Деление простых чисел, операции в столбик, определение остатка — с этой задачей можно справиться и самостоятельно. Если же ученик «проседает» в дробях, то имеет смысл вернуться к истокам и повторно проработать простые арифметические действия.

Оптимальным решением станет обращение за помощью к квалифицированному педагогу, который поможет выявить причину сложностей и помочь с вычислениями. Например, найти в Запорожье курсы ментальной арифметики, благодаря которым цифры перестанут быть для детей чем-то пугающим, а большинство операций будут проводиться в уме. Такая подготовка позволит легко работать с дробями, выполняя сложение/вычитание, умножение/деление.

Деление дробей

Дробь — это число, которое состоит из нескольких частей. Например, всего 6 кусков торта: 66 , всего 6 и берем все эти 6 кусков. Если же всего 6, но взяли мы только 3, то дробь будет выглядеть: 36.

Для деления обыкновенных дробей используется метод перекрестных действий:

• числитель первого числа умножаем на знаменатель другого — результат станет числителем частного;

• знаменатель второго числа умножаем на числитель первого — результат становится знаменателем частного.

Сложность в том, что для деления используется умножение — это как раз обычно и смущает школьников. Поэтому правило нужно просто заучить, повторив его многократно и отработав на многочисленных примерах. Только в этом случае дети запоминают, что когда речь идет о дробях, для деления используется умножение (перемножаем расположенные по диагонали числа, а результат записываем в числитель/знаменатель частного).

Деление произведения на число

Произведение можно разделить на число двумя способами:

1) Чтобы разделить произведение на какое-нибудь число, можно сначала вычислить значение произведения (выполнить умножение) и полученный результат разделить.

Например, чтобы найти значение выражения:

(12 · 5) : 3,

можно сначала умножить  12  на  5:

12 · 5 = 60

и полученное произведение разделить на  3:

60 : 3 = 20,

значит  (12 · 5) : 3 = 60 : 3 = 20.

Если один из сомножителей делится на число, на которое надо разделить произведение, то можно воспользоваться вторым способом нахождения частного от деления произведения на число.

2) Чтобы разделить произведение на какое-нибудь число, можно разделить на это число один любой сомножитель, оставив другие без изменений.

Например, чтобы найти значение выражения:

(8 · 20) : 4,

можно сначала разделить любой из сомножителей  (8  или  20)  на  4:

8 : 4 = 2

и полученное частное умножить на другой сомножитель:

2 · 20 = 40,

значит  (8 · 20) : 4 = (8 : 4) · 20 = 2 · 20 = 40.

Данное выражение можно решить ещё так:

(8 · 20) : 4 = 8 · (20 : 4) = 8 · 5 = 40.

Разделение ячеек с помощью инструмента разделения текста Split text.

Теперь, когда вы знакомы со встроенными функциями, позвольте мне показать вам альтернативный способ разделения ячеек в Excel. Я имею в виду инструмент « , включенный в Ultimate Suite for Excel . Он может выполнять следующие операции:

• Разделить ячейку по символам
• Разделить ячейку по строке
• Разделить ячейку по маске (шаблону)

Например, разделение сведений об участнике из одной ячейки в несколько можно выполнить за 2 быстрых шага. Вот пример исходных данных:

1. Выделите ячейки, которые хотите разделить, и щелкните значок «Разделить текст (Split Text)» на вкладке «Ablebits Data» в разделе «Текст».

1. На панели «Разделить текст» настройте следующие параметры:
   • Выберите в качестве разделителей запятую и пробел.
   • Установите флажок Считать последовательные разделители одним.
   • В разделе «Выбор способа разделения ячеек» выберите «Разбить на столбцы (Split by columns)».
   • Нажмите кнопку «Разделить (Split)» .

Готово! Между исходными столбцами вставляются четыре новых столбца с разделенными данными, и вам нужно только дать этим столбцам соответствующие имена:

Совет: Инструмент «Разделить текст» предоставляет еще два параметра для разделения ячейки в Excel. Дополнительные сведения см. В  и « . 

Если вам интересно увидеть в действии инструменты «Разделить текст» и «Разделить имена» , можете загрузить 14-дневную пробную версию  Ultimate Suite for Excel. 

Благодарю вас за чтение и надеюсь увидеть вас в нашем блоге на следующей неделе!

Деление на число, оканчивающееся нулями

Разделяя число 27057 на 400 и поступая при этом по общему правилу

мы замечаем, что две последние цифры делимого не оказывают никакого влияния на частное. Они являются в остатке без всякой перемены. Откуда правило:

Если делитель оканчивается нулями, отделяют в делимом запятою от правой руки к левой столько цифр, сколько зачеркнуто нулей в делителе, и делят часть делимого до запятой на значащие цифры делителя. Отделенные цифры делимого приписывают к остатку.

В данном примере деление представится в виде

f

Если делимое и делитель оканчиваются нулями, их зачеркивают поровну в делимом, делителе и производят деление; зачеркнутые нули делимого приписывают к остатку.

Чтобы разделить 27300 на 4100, делим 273 на 41:

Частное будет 6, а остаток 2700.

Число цифр частного. При делении отделяют в делимом от левой руки к правой столько цифр, сколько их находится во делителе, или одною больше. Каждой оставшейся цифре делимого соответствует особая цифра частного, следовательно, число цифр частного будет равно или разности числа цифр делимого и делителя или на единицу больше этой разности.

Способ 2: деление содержимого ячеек

Также в Excel можно делить данные, находящиеся в ячейках.

1. Выделяем в ячейку, в которую будет выводиться результат вычисления. Ставим в ней знак «=». Далее кликаем по месту, в котором расположено делимое. За этим её адрес появляется в строке формул после знака «равно». Далее с клавиатуры устанавливаем знак «/». Кликаем по ячейке, в которой размещен делитель. Если делителей несколько, так же как и в предыдущем способе, указываем их все, а перед их адресами ставим знак деления.

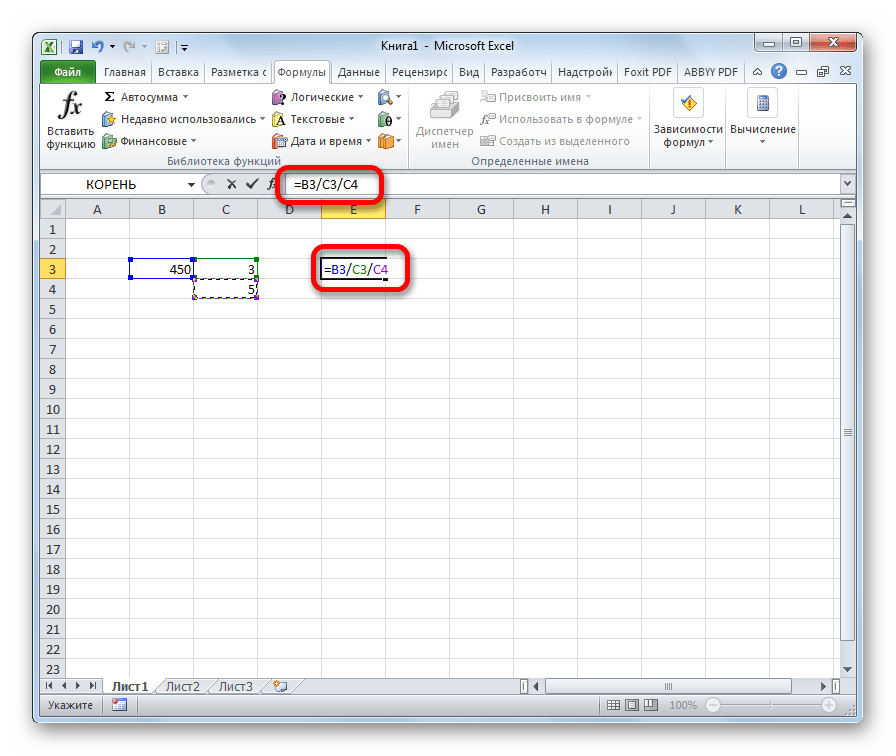
Для того, чтобы произвести действие (деление), кликаем по кнопке «Enter».

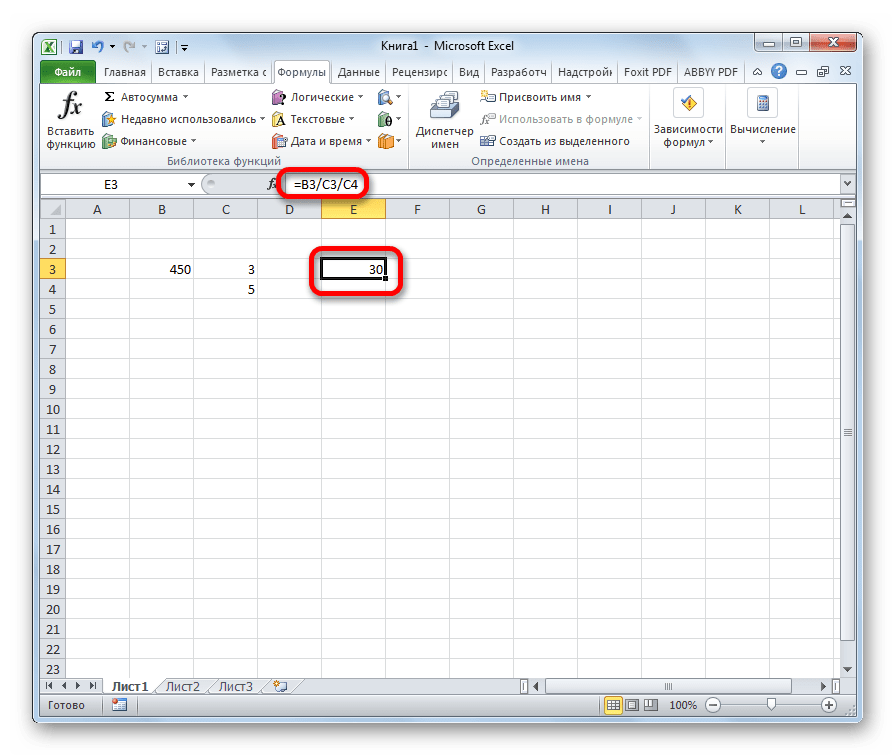
Можно также комбинировать, в качестве делимого или делителя используя одновременно и адреса ячеек и статические числа.

Деление на 10, 100, 1000 и т. д.

Разделяя число на 10, мы десятки делимого обращаем в единицы, сотни в десятки, тысячи в сотни, вообще понижаем на единицу все порядки делимого. Этого мы достигаем, отделяя запятою цифру единиц. Число до запятой будет выражать частное, а после запятой — остаток.

Разделяя на 100, мы понижаем все порядки делимого на две единицы, для чего отделяем запятою от правой руки к левой две цифры и т. д. Отсюда правило:

Чтобы разделить какое-нибудь число на единицу с нулями, нужно от правой руки к левой отделить столько цифр, сколько нулей в делителе; тогда число до запятой выражает целое частное, а после запятой — остаток.

Пример. Разделяя 30207 на 100. Отделяя справа 2 цифры, находим 302,07. Целое частное будет 302, а остаток 7.

Юридическая помощь при разделе дома

Осуществляя раздел дома, обязательно необходимо заручится поддержкой квалифицированного юриста.

Причин несколько:

• Во-первых, стоимость недвижимости довольно высока, чтобы рисковать таким имуществом, осуществляя раздел без квалифицированной помощи.
• Во-вторых, юрист сможет наиболее полноценно защитить интересы клиента, удовлетворить его требования. Профессионалы видят ситуацию несколько иначе, чем обыватели, не имеющие юридического образования. Можно сказать, что профессионалы видят больше.

Таким образом, если проводить раздел дома при помощи юриста, то процедура пройдет быстрее, а ее результат будет более выгодным для клиента.

Когда делитель больше делимого

Вызывают затруднение случаи, когда делитель получается больше делимого. Десятичные дроби в программе за 3 класс еще не изучаются, но, следуя логике, ответ надо записывать в виде дроби – в лучшем случае десятичной, в худшем – простой. Но (!) помимо программы, методику вычисления ограничивает поставленная задача: необходимо не разделить, а найти остаток! Дробная часть им не является! Как решить такую задачу?

Обратите внимание! Существует правило для случаев, когда делитель больше делимого: неполное частное равно 0, остаток равен делимому. Как разделить число 5 на число 6, выделив остаток? Сколько 6-литровых банок влезет в пятилитровую? Ноль, потому что 6 больше 5

Как разделить число 5 на число 6, выделив остаток? Сколько 6-литровых банок влезет в пятилитровую? Ноль, потому что 6 больше 5.

По заданию необходимо заполнить 5 литров – не заполнено ни одного. Значит, остались все 5. Ответ: неполное частное = 0, остаток = 5.

Деление начинают изучать в третьем классе школы. К этому времени ученики уже должны освоить таблицу умножения, что позволяет им совершать деление двузначных чисел на однозначные.

Решите задачу: 18 конфет нужно раздать пятерым детям. Сколько конфет останется?

Примеры:

14:3

Находим неполное частное: 3*1=3, 3*2=6, 3*3=9, 3*4=12, 3*5=15. 5 – перебор. Возвращаемся к 4.

Остаток: 3*4=12, 14-12=2.

Ответ: неполное частное 4, осталось 2.

Вы можете спросить, почему при делении на 2, остаток либо равен 1, либо 0. По таблице умножения, между цифрами, кратными двум существует разница в единицу.

Еще одна задача: 3 пирожка надо разделить на двоих.

4 пирожка разделить на двоих.

5 пирожков разделить на двоих.

Связь деления с умножением

Чтобы проследить связь между делением и умножением, вспомним, что деление представляется, как разбиение исходного делимого множества на несколько одинаковых множеств. Умножение связано с объединением нескольких одинаковых множеств в одно. 

Деление — действие, обратное умножению. Что это значит? Приведем аналогию. Представим, что у нас есть b множеств, в каждом из которых — по с предметов. Общее количество предметов во всех множествах равно a. Умножение — это объединение всех множеств в одно. Математически оно запишется так:

b·c=a.

Обратный процесс разбиения полученного общего множества на b множеств по с предметов в каждом соответствует делению:

a÷b=c.

На основе сказанного можно перейти к следующему утверждению:

Если произведение натуральных чисел c и b равно a, то частное чисел a и b равно c. Перепишем в буквенном виде. 

Если b·c=a, то a÷b=c

Пользуясь переместительным свойством умножения, можно записать:

c·b=a

Отсюда также следует, что a÷с=b. 

На основании сказанного можно сформулировать общий вывод. Если произведение чисел c и b равно a, то соответственно частные a÷b и a÷c равны c и b.

Подытожим все изложенное выше и дадим определение деления натуральных чисел.

Деление натуральных чисел

Деление — нахождение неизвестного множителя по известному произведению и другому известному множителю.

Это определение станет базой, на основе которой мы будем строить правила и методы деления натуральных чисел.

Как разбить текст по переносам строки.

Чтобы разделить слова в ячейке по переносам строки, используйте подходы, аналогичные тем, которые были продемонстрированы в предыдущем примере. Единственное отличие состоит в том, что вам понадобится функция СИМВОЛ (CHAR) для передачи символа разрыва строки, поскольку вы не можете ввести его непосредственно в формулу с клавиатуры.

Предположим, ячейки, которые вы хотите разделить, выглядят примерно так:

Напомню, что перенести таким вот образом текст внутри ячейки можно при помощи комбинации клавиш ALT + ENTER.

Возьмите инструкции из предыдущего примера и замените дефис («-») на СИМВОЛ(10), где 10 — это код ASCII для перевода строки.

Чтобы извлечь наименование товара:

Цвет:

Размер:

Результат вы видите на скриншоте выше.

Таким же образом можно работать и с любым другим символом-разделителем. Достаточно знать его код.

Проверка результата деления целых чисел

Проверку осуществляют умножением. Чтобы произвести проверку деления, нужно полученное частное умножить на делитель, если  в результате получается число, равное делимому, тогда результат считается правильным.

Рассмотрим на примере решение с проверкой результата.

Пример 6

Результат деления 72 на -9 равен -7. Произвести проверку данного выражения.

Решение

Выполняем проверку деления. Необходимо произвести умножение полученного частного и делителя, то есть (−7)·(−9)=63. Проверка показала, что 63 отлично от 72, значит действие выполнено неверно.

Ответ: деление выполнено неверно.

Всё ещё сложно?
Наши эксперты помогут разобраться

Все услуги

Решение задач

от 1 дня / от 150 р.

Курсовая работа

от 5 дней / от 1800 р.

Реферат

от 1 дня / от 700 р.

Разделы: какие и сколько нужны?

Собственно, никаких ограничений здесь нет. Разве что с точки зрения здравого смысла. Многое зависит от объема вашего диска. Например, террабайтник не стоит делить больше, чем на 2 раздела. Диски от 2 Тбайт можно «порезать» и на 3

Важно лишь понять, для чего они будут служить. Вот один из возможных вариантов деления. 

• Системный (от 500 Гбайт) — для работы системы и софта;
• Основной — для хранения файлов, документов;
• Медиа — для хранения фильмов, фотографий, видео;
• Игры — тут без комментариев. 

Слишком много разделов тоже плохо — скорее всего, они будут маленькими и быстро начнут переполняться. 

Деление многозначного числа на многозначное

При делении многозначного числа на многозначное поступаем точно так же, как поступали при делении многозначного числа на однозначное.

Разделяя число 37207 на 47, мы прежде всего определяем, из скольких цифр состоит частное. Частное меньше 1000 и больше 100, ибо 37207 меньше 47000 (47 × 1000) и больше 4700 (47 × 100), следовательно, частное состоит из сотен, десятков и единиц. Начиная с сотен, мы определяем каждую цифру частного отдельно:

1. Определяем сотни частного:

   Делимое 37207 имеет 372 сотни. Десятки и единицы делимого не имеют влияния на цифру сотен частного. В частном может быть только 7 сотен, ибо 47 содержится в 372 семь раз; пишем в частном 700.

   Умножая делитель на частное и вычитая из делимого, получаем первый остаток 4307.

2. Определяем десятки частного:

   Остаток 4307 содержит 430 десятков. Единицы не имеют влияния на цифру десятков частного. Делитель 47 содержится в 430 девять раз; пишем в частном 90.

   Умножая 90 на частное 47 и вычитая произведение 4330, получаем в остатке 77.

3. Определяем единицы частного:

   47 содержится в 77 один раз. Пишем в частном 1 и, вычитая из 77 произведение единицы на делитель, получаем в остатке 30.

Итак, после деления имеем в целом частном 791 и в остатке 30.

Если не писать каждый раз лишних нулей и принимать в соображение только те цифры делимого, которые имеют влияние на частное, ход вычисления изобразится письменно:

словесно:

1. Отделяем в делимом от левой руки к правой столько цифр, чтобы делитель мог содержаться в отделенной части делимого. В данном случае отделяем 3 цифры, 47 содержится в 372 семь раз; умножаем делитель 47 на 7, цифру частного, и, вычитая произведение 47 × 7 = 329 из 372, получаем в остатке 43.

2. К остатку 43 сносим 0, следующую цифру делимого; 47 содержится в 430 девять раз, пишем в частном 9. Умножая 47 на 9 и вычитая произведение 423 из 430, получаем остаток 7.

3. Сносим к остатку следующую цифру частного 7; 47 содержится в 77 один раз. Пишем единицу в частном.

Умножая ею делитель и вычитая 47 из 77, получаем в остатке 30 и в целом частно 791.

Пример. Разделить 671064 на 335. Деление изобразится письменно:

словесно:

1. Отделяем 671 в делимом; 335 содержится в 671 два раза, пишем в частном 2. Умножая 335 на 2 и вычитая произведение 670, получим в остатке 1.

2. Сносим 0, следующую цифру делимого; 335 не содержится в 10, — пишем для второй цифры частного 0.

3. Сносим 6, следующую цифру делимого; 335 не содержится в 106, — пишем для третьей цифры частного 0.

4. Сносим следующую цифру делимого 4; 335 содержится в 1064 три раза, — пишем в частном 3. Умножая делитель на 3 и вычитая произведение, получим в остатке 59 и в целом частном 2003.

Из предложенных примеров выводим следующее правило:

1. Чтобы разделить многозначное число на однозначное или многозначное, нужно отделить в делимом от левой руки к правой столько цифр, сколько их находится в делителе. Если делитель не содержится, отделяют в делимом одной цифрой больше. Разделив отделенное число на делитель, получают первую цифру частного, умножают ей делитель и полученное произведение вычитают из отделенной части делимого.

2. К остатку сносят следующую цифру делимого и снова задаются.

3. Если при этом получается число меньше делителя, пишут в частном нуль, сносят следующую цифру и снова задаются.

4. Получив новую цифру частного, поступают с нею так же, как и с первой цифрой.

5. Деление продолжают до тех пор, пока не снесут всех цифр делимого и не получат таким образом всех цифр частного.

Всякий раз, когда приходится делить, нужно задаваться в частном такою цифрой, чтобы остаток был меньше делителя

Чтобы легче найти такую цифру частного, при делении многозначного числа на многозначное обращают внимание на одну или две старшие цифры делителя и задаются только ими в соответствующей части делимого. При этом в делимом и в делителе отделяют от правой руки к левой одинаковое число цифр

Так, определяя, сколько раз содержится 6373 в 27302, мы задаемся четырьмя, ибо 6 в 27 содержится 4 раза.

Полученная при этом цифра частного будет или равна или больше действительной. В последнем случае ее нужно уменьшить.

Иногда при делении не подписывают произведение цифры частного на делитель, а, подразумевая его в уме, подписывают один остаток. Сокращая таким образом деление, изображают его письменно:

словесно:

1. 8 в 43 содержится 5 раз; 5-ю 8 — сорок. Вычитая 40 из 43, получаем в остатке 3.

2. Сносим 2; 8 в 32 содержится 4 раза; 4-жды 8 составляет 32. Вычитая 32, получим в остатке нуль.

3. Сносим 8; 8 в 8-ми содержится 1 раз, 1-жды 8 составляет 8. Вычитая 8, получаем в остатке нуль и в частном 541.

Как разбить ячейку с помощью формул

Какую бы разнообразную информацию ни содержала ваша таблица, формула для разделения ячейки в Excel сводится к нахождению позиции разделителя (запятая, пробел и т. д.).  А затем уже мы извлекаем подстроку до, после или между разделителями. Как правило, вам нужно использовать функции ПОИСК или НАЙТИ для определения местоположения разделителя и одну из текстовых функций ( ЛЕВСИМВ, ПРАВСИМВ или ПСТР) для получения подстроки.

Например, вы должны использовать следующие формулы для разделения данных в A2, разделенных пробелом (см. скриншот ниже):

Чтобы извлечь артикул в B2:

Чтобы извлечь название товара в C2:

Более подробно о разделении ячейки при помощи формул читайте здесь.

Деление с остатком целых отрицательных чисел

Сформулируем правило деления с остатком целых отрицательных чисел:

Для получения неполного частного с от деления целого отрицательного числа a на целое отрицательное b, нужно произвести вычисления по модулю, после чего прибавить 1. Тогда можно произвести вычисления по формуле: d = a − b * c

Из правила следует, что неполное частное от деления целых отрицательных чисел — положительное число.

Алгоритм деления с остатком целых отрицательных чисел:

• найти модули делимого и делителя;
• разделить модуль делимого на модуль делителя;
• получить неполное частное и остаток;
• прибавить 1 к неполному частному;
• вычислить остаток, исходя из формулы d = a − b * c.

Пример

Найти неполное частное и остаток при делении −17 на −5.

Как решаем:

Применим алгоритм для деления с остатком.

Разделим числа по модулю. Получим, что неполное частное равно 3, а остаток равен 2.

Сложим неполное частное и 1: 3 + 1 = 4. Из этого следует, что неполное частное от деления заданных чисел равно 4.

Для вычисления остатка применим формулу. По условию a = −17, b = −5, c = 4, тогда получим d = a − b * c = −17 − (−5) * 4 = −17 − (−20) = −17 + 20 = 3.

Получилось, что остаток равен 3, а неполное частное равно 4.

Ответ: (−17) : (−5) = 4 (остаток 3).

Для чего это может быть полезно?

Ничто так ярко не иллюстрирует преимущества отдельных функций, как реальные примеры использования. Допустим, вы являетесь студентом и пишете курсовую работу. Разумеется, вы вынуждены использовать источники (например, из интернета), попутно набирая текст в редакторе.

Без режима двойного экрана вам придется постоянно переключаться между программой с источником и текстом работы. А при помощи рассматриваемой функции вы сэкономите время, отказавшись от частых переключений, поскольку оба окна в равной степени будут отображаться на главном экране.

Можно привести и более «приземленный» пример, который знаком любому геймеру. Человек запускает на YouTube видеоролик с прохождением и попутно пытается повторить действия в игре. В ситуации, когда программы открыты в разных окнах, речь не идет о комфорте. Процесс затягивается, и геймер вынужден после каждого шага ставить игру на паузу. Разделение экрана полностью решает эту проблему.

Включив воображение, вы и сами сможете привести еще, по меньшей мере, 5-10 примеров подобного толка. Все будет зависеть от сценариев работы за компьютером. Но одно остается неизменным – функция двойного экрана крайне важна, как в процессе потребления контента, так и при работе на ПК.

Основы деления десятичных дробей

Все десятичные дроби, как конечные, так и периодические, представляют из себя всего лишь особую форму записи обыкновенных дробей. Следовательно, на них распространяются те же принципы, что и на соответствующие им обыкновенные дроби. Таким образом, весь процесс деления десятичных дробей мы сводим к замене их на обыкновенные с последующим вычислением уже известными нам способами. Возьмем конкретный пример.

Пример 1

Разделите 1,2 на ,48.

Решение

Запишем десятичные дроби в виде обыкновенных. У нас получится:

1,2=1210=65

,48=48100=1225.

Таким образом, нам надо разделить 65 на 1225. Считаем:

1,2,48=621225=65·2512=6·255·12=52

Из получившейся в итоге неправильной дроби можно выделить целую часть и получить смешанное число 212, а можно представить ее в виде десятичной дроби, чтобы она соответствовала исходным цифрам: 52=2,5. О том, как это сделать, мы уже писали ранее.

Ответ: 1,2,48=2,5. 

Пример 2

Посчитайте, сколько будет ,(504),56.

Решение

Для начала нам нужно перевести периодическую десятичную дробь в обыкновенную.

,(504)=,5041-,001=,504,999=504999=56111

После этого конечную десятичную дробь также переведем в другой вид: ,56=56100. Теперь у нас есть два числа, с которыми нам будет легко провести необходимые вычисления:

,(504)1,11=5611156100=56111·10056=100111

У нас получился результат, который мы также можем перевести в десятичный вид. Для этого разделим числитель на знаменатель, используя метод столбика:

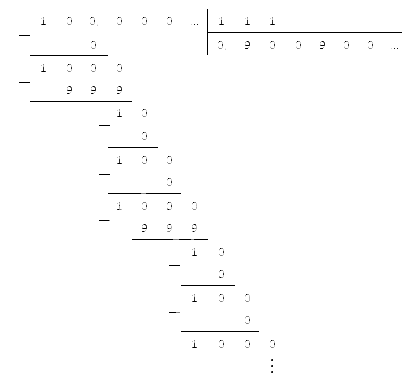
Ответ: ,(504),56=,(900). 

Если же в примере на деление нам встретились непериодические десятичные дроби, то мы будем действовать немного иначе. Мы не можем их привести к привычным обыкновенным дробям, поэтому при делении приходится предварительно округлять их до определенного разряда. Это действие должно быть выполнено как с делимым, так и с делителем: имеющуюся конечную или периодическую дробь в интересах точности мы тоже будем округлять.

Пример 3

Найдите, сколько будет ,779…1,5602.

Решение 

Первым делом мы округляем обе дроби до сотых. Так мы переходим от бесконечных непериодических дробей к конечным десятичным:

,779…≈,78

1,5602≈1,56

Можем продолжить подсчеты и получить примерный результат: ,779…1,5602≈,781,56=78100156100=78100·100156=78156=12=,5.

Точность результата будет зависеть от степени округления.

Ответ: ,779…1,5602≈,5.

Деление разности на число

Разность можно разделить на число двумя способами:

1) Чтобы разделить разность на какое-нибудь число, можно сначала вычислить значение разности (выполнить вычитание) и полученный результат разделить.

Например, чтобы найти значение выражения:

(24 — 8) : 2,

можно сначала вычесть из  24  число  8:

24 — 8 = 16,

и полученную разность разделить на  2:

16 : 2 = 8,

значит  (24 — 8) : 2 = 16 : 2 = 8.

Если и уменьшаемое и вычитаемое в записи разности делятся на число, на которое надо разделить разность, то можно воспользоваться вторым способом нахождения частного от деления разности на число.

2) Чтобы разделить разность на какое-нибудь число, можно разделить на это число отдельно уменьшаемое и вычитаемое, а потом из первого частного вычесть второе.

Например, чтобы найти значение выражения:

(42 — 28) : 7,

можно отдельно уменьшаемое и вычитаемое разделить на число  7:

42 : 7 = 6,   28 : 7 = 4

и найти разность полученных частных:

6 — 4 = 2,

значит  (42 — 28) : 7 = 42 : 7 — 28 : 7 = 6 — 4 = 2.